Sujets de Bac
2025
Filtrer par chapitre
Amerique Du Nord 21 Mai 2025 Jour 1
4 exercices
Pour accéder au réseau privé d'une entreprise depuis l'extérieur, les connexions des employés transitent aléatoirement via trois serveurs distants différents, notés A, B et C. Ces serveurs ont des caractéristiques techniques différentes et les connexions se répartissent de la manière suivante :
- 25% des connexions transitent via le serveur A;
- 15% des connexions transitent via le serveur B;
- le reste des connexions s'effectue via le serveur C.
Les connexions à distance sont parfois instables et, lors du fonctionnement normal des serveurs, les utilisateurs peuvent subir des déconnexions pour différentes raisons (saturation des serveurs, débit internet insuffisant, attaques malveillantes, mises à jour de logiciels, etc.).
On dira qu'une connexion est stable si l'utilisateur ne subit pas de déconnexion après son identification aux serveurs. L'équipe de maintenance informatique a observé statistiquement que, dans le cadre d'un fonctionnement habituel des serveurs :
- 90% des connexions via le serveur A sont stables;
- 80% des connexions via le serveur B sont stables;
- 85% des connexions via le serveur C sont stables.
Les parties A et B sont indépendantes l'une de l'autre et peuvent être traitées séparément.
Partie A
On s'intéresse au hasard à l'état d'une connexion effectuée par un employé de l'entreprise. On considère les évènements suivants :
- $A$ : "La connexion s'est effectuée via le serveur A";
- $B$ : "La connexion s'est effectuée via le serveur B";
- $C$ : "La connexion s'est effectuée via le serveur C";
- $S$ : "La connexion est stable".
On note $\overline{S}$ l'évènement contraire de l'évènement $S$.
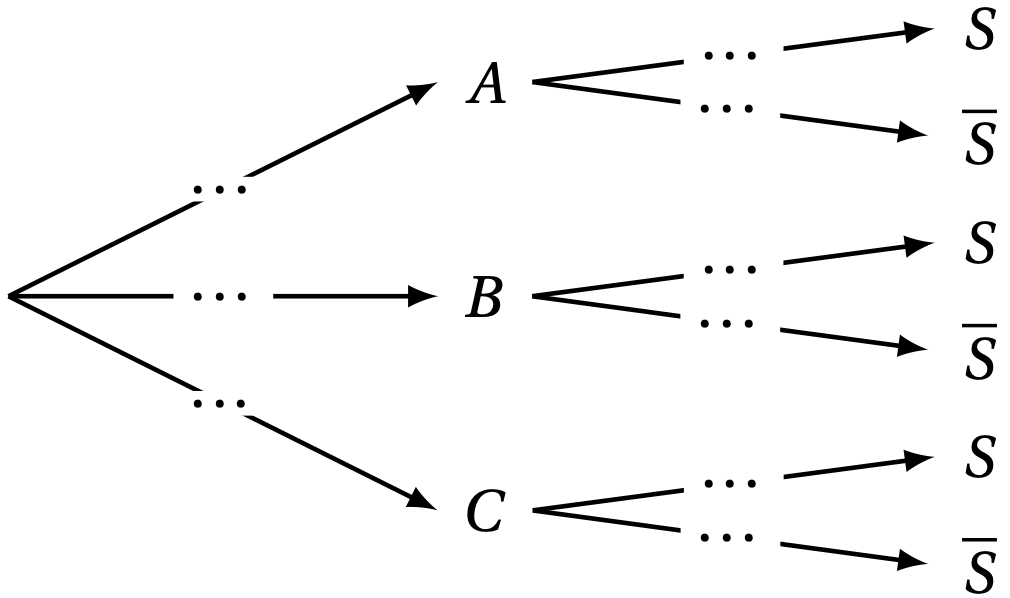
- Recopier et compléter l'arbre pondéré ci-dessous modélisant la situation de l'énoncé.
- Démontrer que la probabilité que la connexion soit stable et passe par le serveur B est égale à $0,12$.
- Calculer la probabilité $P\left(C \cap \overline{S}\right)$ et interpréter le résultat dans le contexte de l'exercice.
- Démontrer que la probabilité de l'évènement $S$ est $P(S) = 0,855$.
- On suppose désormais que la connexion est stable.
Calculer la probabilité que la connexion ait eu lieu depuis le serveur B.
On donnera la valeur arrondie au millième.
Partie B
D'après la partie A, la probabilité qu'une connexion soit instable est égale à $0,145$.
- Dans le but de détecter les dysfonctionnements de serveurs, on étudie un échantillon de 50 connexions au réseau, ces connexions étant choisies au hasard. On suppose que le nombre de connexions est suffisamment important pour que ce choix puisse être assimilé à un tirage avec remise.
On désigne par $X$ la variable aléatoire égale au nombre de connexions instables au réseau de l'entreprise, dans cet échantillon de 50 connexions.- On admet que la variable aléatoire $X$ suit une loi binomiale. Préciser ses paramètres.
- Donner la probabilité qu'au plus huit connexions soient instables. On donnera la valeur arrondie au millième.
- Dans cette question, on constitue désormais un échantillon de $n$ connexions, toujours dans les mêmes conditions, où $n$ désigne un entier naturel strictement positif. On note $X_{n}$ la variable aléatoire égale aux nombres de connexions instables et on admet que $X_{n}$ suit une loi binomiale de paramètres $n$ et $0,145$.
- Donner l'expression en fonction de $n$ de la probabilité $p_{n}$ qu'au moins une connexion de cet échantillon soit instable.
- Déterminer, en justifiant, la plus petite valeur de l'entier naturel $n$ telle que la probabilité $p_{n}$ est supérieure ou égale à $0,99$.
- On s'intéresse à la variable aléatoire $F_{n}$ égale à la fréquence de connexions instables dans un échantillon de $n$ connexions, où $n$ désigne un entier naturel strictement positif.
On a donc $F_{n}=\dfrac{X_{n}}{n}$, où $X_{n}$ est la variable aléatoire définie à la question 2.- Calculer l'espérance $E\left(F_{n}\right)$.
On admet que $V\left(F_{n}\right)=\dfrac{0,123975}{n}$. - Vérifier que : $P\left(\left|F_{n}-0,145\right| \geqslant 0,1\right) \leqslant \dfrac{12,5}{n}$
- Un responsable de l'entreprise étudie un échantillon de 1000 connexions et constate que pour cet échantillon $F_{1000}=0,3$. Il soupçonne un dysfonctionnement des serveurs. A-t-il raison ?
- Calculer l'espérance $E\left(F_{n}\right)$.
On considère la suite numérique $(u_{n})$ définie par son premier terme $u_{0}=2$ et pour tout entier naturel $n$, par : $$u_{n+1}=\dfrac{2 u_{n}+1}{u_{n}+2}$$
On admet que la suite $(u_{n})$ est bien définie.
- Calculer le terme $u_{1}$.
- On définit la suite $(a_{n})$ pour tout entier naturel $n$, par :
$$a_{n}=\dfrac{u_{n}}{u_{n}-1}$$
On admet que la suite $(a_{n})$ est bien définie.
- Calculer $a_{0}$ et $a_{1}$.
- Démontrer que, pour tout entier naturel $n$, $a_{n+1}=3 a_{n}-1$.
- Démontrer par récurrence que, pour tout entier naturel $n$ supérieur ou égal à 1, $$a_{n} \geqslant 3 n-1$$
- En déduire la limite de la suite $(a_{n})$.
- On souhaite étudier la limite de la suite $(u_{n})$.
- Démontrer que pour tout entier naturel $n$, $u_{n}=\dfrac{a_{n}}{a_{n}-1}$.
- En déduire la limite de la suite $(u_{n})$.
- On admet que la suite $(u_{n})$ est décroissante.
On considère le programme suivant écrit en langage Python :def algo(p): u=2 n=0 while u-1>p: u=(2*u+1)/(u+2) n=n+1 return (n,u)- Interpréter les valeurs n et u renvoyées par l'appel de la fonction algo(p) dans le contexte de l'exercice.
- Donner, sans justifier, la valeur de $n$ pour $p=0,001$.
Pour chacune des affirmations suivantes, indiquer si elle est vraie ou fausse. Chaque réponse doit être justifiée. Une réponse non justifiée ne rapporte aucun point.
L'espace est rapporté à un repère orthonormé $(O;\vec{i},\vec{j},\vec{k})$.
On considère la droite $(d)$ dont une représentation paramétrique est :
$$\left\{\begin{array}{l c l} x&=&3 - 2 t \\ y&=&-1 \\ z&=&2 - 6 t \end{array} \quad, \text{ où } t \in \mathbb{R}\right.$$On considère également les points suivants :
- A$(3~;~-3~;~-2)$
- B$(5~;~-4~;~-1)$
- C le point de la droite $(d)$ d'abscisse 2
- H le projeté orthogonal du point B sur le plan $\mathcal{P}$ d'équation $x + 3z -7 = 0$
Affirmation 1
La droite $(d)$ et l'axe des ordonnées sont deux droites non coplanaires.
Affirmation 2
Le plan passant par $A$ et orthogonal à la droite $(d)$ a pour équation cartésienne :
$$x + 3z + 3= 0$$Affirmation 3
Une mesure, exprimée en radian, de l'angle géométrique $\widehat{\mathrm{BAC}}$ est $\dfrac{\pi}{6}$.
Affirmation 4
La distance BH est égale à $\dfrac{\sqrt{10}}{2}$.
La partie C est indépendante des parties A et B.
Partie A
On donne ci-dessous, dans un repère orthogonal, les courbes $\mathcal{C}_{1}$ et $\mathcal{C}_{2}$, représentations graphiques de deux fonctions définies et dérivables sur $\mathbb{R}$. L'une des deux fonctions représentées est la fonction dérivée de l'autre. On les notera $g$ et $g'$.
On précise également que :
- La courbe $\mathcal{C}_{1}$ coupe l'axe des ordonnées au point de coordonnées $(0~;~1)$.
- La courbe $\mathcal{C}_{2}$ coupe l'axe des ordonnées au point de coordonnées $(0~;~2)$ et l'axe des abscisses aux points de coordonnées $(-2~;~0)$ et $(1~;~0)$.
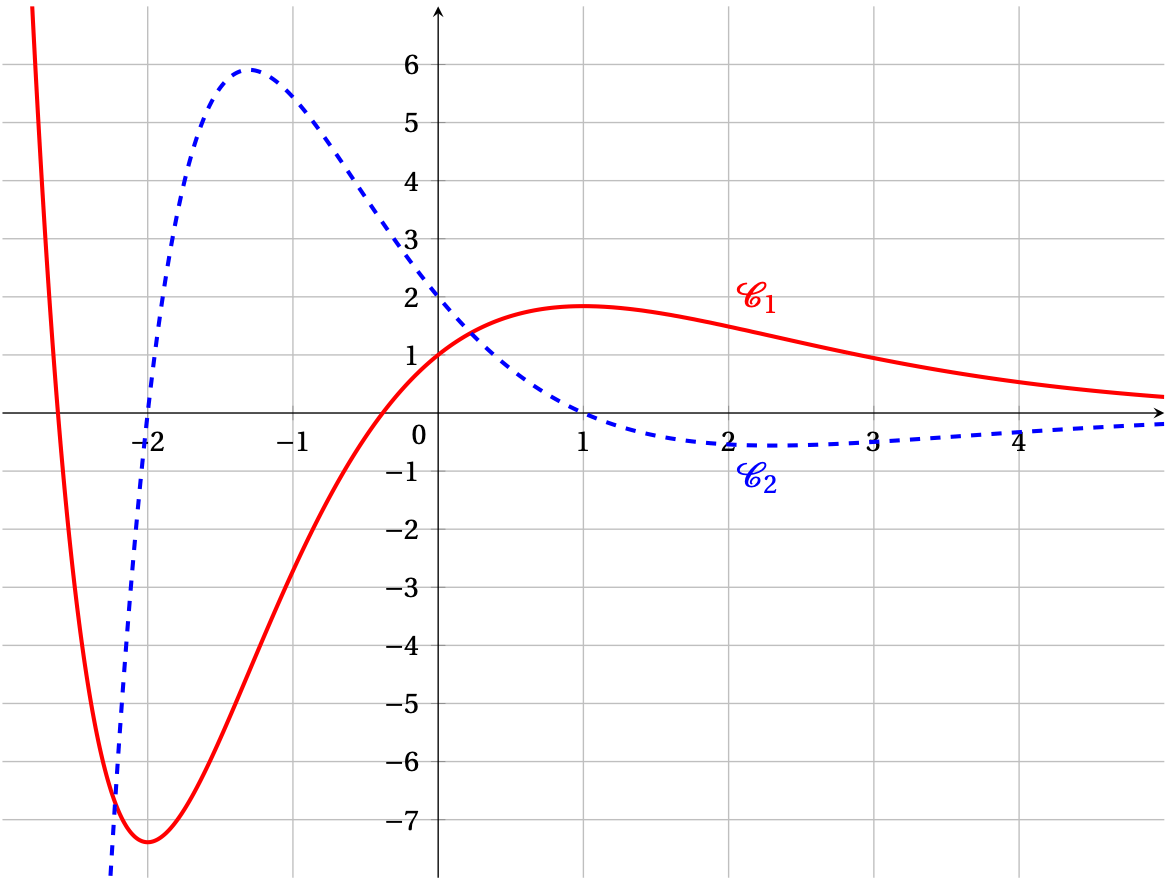
- En justifiant, associer à chacune des fonctions $g$ et $g'$ sa représentation graphique.
- Justifier que l'équation réduite de la tangente à la courbe représentative de la fonction $g$ au point d'abscisse 0 est $y=2x + 1$.
Partie B
On considère $(E)$ l'équation différentielle
$$y+y'=(2x + 3) \mathrm{e}^{-x},$$où $y$ est une fonction de la variable réelle $x$.
- Montrer que la fonction $f_{0}$ définie pour tout nombre réel $x$ par $f_{0}(x)=\left(x^{2}+3 x\right) \mathrm{e}^{-x}$ est une solution particulière de l'équation différentielle $(E)$.
- Résoudre l'équation différentielle $\left(E_{0}\right): y+ y'= 0$.
- Déterminer les solutions de l'équation différentielle $(E)$.
- On admet que la fonction $g$ décrite dans la partie A est une solution de l'équation différentielle $(E)$.
Déterminer alors l'expression de la fonction $g$. - Déterminer les solutions de l'équation différentielle $(E)$ dont la courbe admet exactement deux points d'inflexion.
Partie C
On considère la fonction $f$ définie pour tout nombre réel $x$ par :
$$f(x)=\left(x^{2}+3 x+2\right) \mathrm{e}^{-x}$$- Démontrer que la limite de la fonction $f$ en $+\infty$ est égale à 0.
On admet par ailleurs que la limite de la fonction $f$ en $-\infty$ est égale à $+\infty$. - On admet que la fonction $f$ est dérivable sur $\mathbb{R}$. On note $f'$ la fonction dérivée de $f$ sur $\mathbb{R}$.
- Vérifier que, pour tout nombre réel $x$, $f'(x)=\left(-x^{2}-x+1\right) \mathrm{e}^{-x}$.
- Déterminer le signe de la fonction dérivée $f'$ sur $\mathbb{R}$ puis en déduire les variations de la fonction $f$ sur $\mathbb{R}$.
- Expliquer pourquoi la fonction $f$ est positive sur l'intervalle $[0;+\infty[$.
- On notera $\mathcal{C}_{f}$ la courbe représentative de la fonction $f$ dans un repère orthogonal $(O;\vec{i},\vec{j})$. On admet que la fonction $F$ définie pour tout nombre réel $x$ par $F(x)=\left(-x^{2}-5 x-7\right) \mathrm{e}^{-x}$ est une primitive de la fonction $f$.
Soit $\alpha$ un nombre réel positif.
Déterminer l'aire $\mathcal{A}(\alpha)$, exprimée en unité d'aire, du domaine du plan délimité par l'axe des abscisses, la courbe $\mathcal{C}_{f}$ et les droites d'équation $x=0$ et $x=\alpha$.
Amerique Du Nord 22 Mai 2025 Jour 2
4 exercices
Au basket-ball, il est possible de marquer des paniers rapportant un point, deux points ou trois points.
Les parties A et B sont indépendantes.
Partie A
L'entraineur d'une équipe de basket décide d'étudier les statistiques de réussite des lancers de ses joueurs. Il constate qu'à l'entrainement, lorsque Victor tente un panier à trois points, il le réussit avec une probabilité de $0,32$.
Lors d'un entrainement, Victor effectue une série de $15$ lancers à trois points. On suppose que ces lancers sont indépendants.
On note $N$ la variable aléatoire qui donne le nombre de paniers marqués.
Les résultats des probabilités demandées seront, si nécessaire, arrondis au millième.
- On admet que la variable aléatoire $N$ suit une loi binomiale. Préciser ses paramètres.
- Calculer la probabilité que Victor réussisse exactement 4 paniers lors de cette série.
- Déterminer la probabilité que Victor réussisse au plus 6 paniers lors de cette série.
- Déterminer l'espérance de la variable aléatoire $N$.
- On note $T$ la variable aléatoire qui donne le nombre de points marqués après cette série de lancers.
- Exprimer $T$ en fonction de $N$.
- En déduire l'espérance de la variable aléatoire $T$. Donner une interprétation de cette valeur dans le contexte de l'exercice.
- Calculer $P(12 \leqslant T \leqslant 18)$.
Partie B
On note $X$ la variable aléatoire donnant le nombre de points marqués par Victor lors d'un match.
On admet que l'espérance $E(X) = 22$ et la variance $V(X) = 65$.
Victor joue $n$ matchs, où $n$ est un nombre entier strictement positif.
On note $X_{1}, X_{2}, \ldots, X_{n}$ les variables aléatoires donnant le nombre de points marqués au cours des $1^{\text{er}}, 2^{\text{e}}, \ldots, n$-ième matchs. On admet que les variables aléatoires $X_{1}, X_{2}, \ldots, X_{n}$ sont indépendantes et suivent la même loi que celle de $X$.
On pose $M_{n}=\dfrac{X_{1} + X_{2} + \ldots + X_{n}}{n}$.
- Dans cette question, on prend $n = 50$.
- Que représente la variable aléatoire $M_{50}$ ?
- Déterminer l'espérance et la variance de $M_{50}$.
- Démontrer que $P\left(\left|M_{50}-22\right| \geqslant 3\right) \leqslant \dfrac{13}{90}$.
- En déduire que la probabilité de l'évènement « $19 < M_{50} < 25$ » est strictement supérieure à 0,85.
- Indiquer, en justifiant, si l'affirmation suivante est vraie ou fausse :
« Il n'existe aucun entier naturel $n$ tel que $P\big(\left|M_{n}-22\right| \geqslant 3\big)< 0,01$ ».
Un des objectifs de cet exercice est de déterminer une approximation du nombre réel $\ln(2)$, en utilisant une des méthodes du mathématicien anglais Henry Briggs au XVIe siècle.
On désigne par $(u_{n})$ la suite définie par :
Partie A
-
- Donner la valeur exacte de $u_{1}$ et de $u_{2}$.
- Émettre une conjecture, à l'aide de la calculatrice, sur le sens de variation et la limite éventuelle de la suite.
-
- Montrer par récurrence que pour tout entier naturel $n$, $1 \leqslant u_{n+1} \leqslant u_{n}$.
- En déduire que la suite $(u_{n})$ est convergente.
- Résoudre dans l'intervalle $[0~;~+\infty[$ l'équation $\sqrt{x} =x$.
- Déterminer, en justifiant, la limite de la suite $(u_{n})$.
Partie B
On désigne par $(v_{n})$ la suite définie pour tout entier naturel $n$ par $v_{n}=\ln \left(u_{n}\right)$.
-
- Démontrer que la suite $(v_{n})$ est géométrique de raison $\dfrac{1}{2}$.
- Exprimer $v_{n}$ en fonction de $n$, pour tout entier naturel $n$.
- En déduire que, pour tout entier naturel $n$, $\ln (2)=2^{n} \ln \left(u_{n}\right)$.
- On a tracé ci-dessous dans un repère orthonormé la courbe $\mathscr{C}$ de la fonction ln et la tangente T à la courbe $\mathscr{C}$ au point d'abscisse 1.
Une équation de la droite T est $y = x - 1$.
Les points $\mathrm{A}_{0}$, $\mathrm{A}_{1}$, $\mathrm{A}_{2}$ ont pour abscisses respectives $u_{0}$, $u_{1}$ et $u_{2}$ et pour ordonnée 0.
On décide de prendre $x - 1$ comme approximation de $\ln (x)$ lorsque $x$ appartient à l'intervalle $]0,99~;~1,01[$.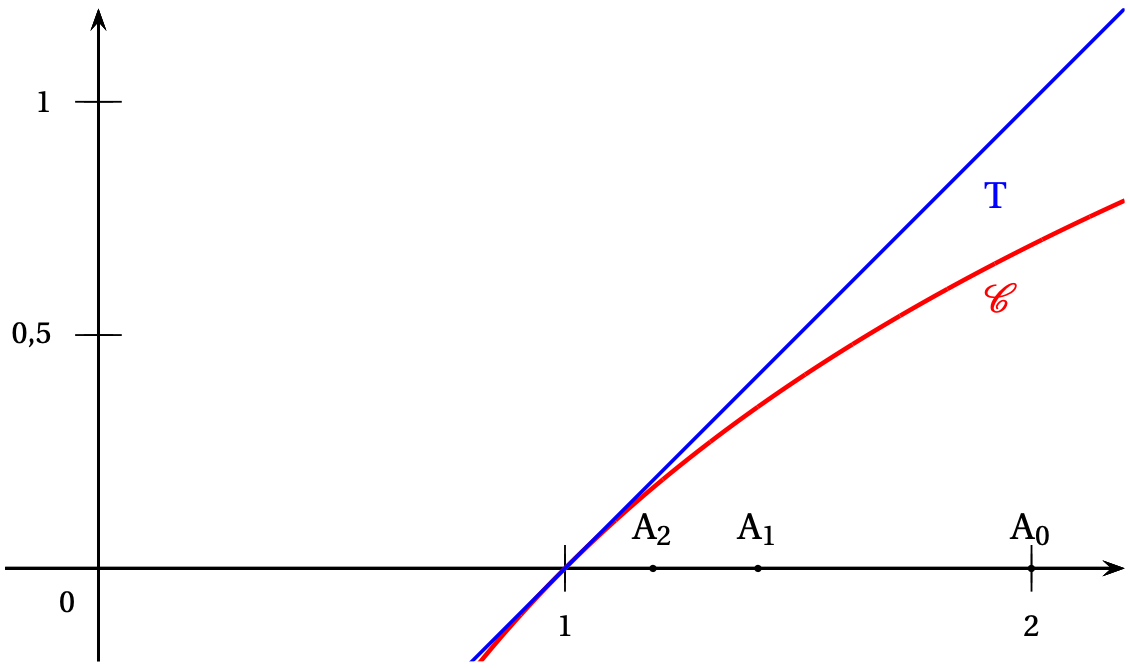
- Déterminer à l'aide de la calculatrice le plus petit entier naturel $k$ tel que $u_{k}$ appartienne à l'intervalle $]0,99 ~;~1,01[$ et donner une valeur approchée de $u_{k}$ à $10^{-5}$ près.
- En déduire une approximation de $\ln \left(u_{k}\right)$.
- Déduire des questions 1. c. et 2. b. de la partie B une approximation de $\ln (2)$.
- On généralise la méthode précédente à tout réel $a$ strictement supérieur à 1.
Recopier et compléter l'algorithme ci-dessous afin que l'appel Briggs(a) renvoie une approximation de $\ln (a)$.
On rappelle que l'instruction en langage Python sqrt(a) correspond à $\sqrt{a}$.from math import* def Briggs(a): n = 0 while a >= 1.01: a = sqrt(a) n = n+1 L =... return L
Pour chacune des affirmations suivantes, indiquer si elle est vraie ou fausse. Chaque réponse doit être justifiée.
Une réponse non justifiée ne rapporte aucun point.
PARTIE A
ABCDEFGH est un cube d'arête de longueur 1.
Les points I, J, K, L et M sont les milieux respectifs des arêtes [AB], [BF], [AE], [CD] et [DH].
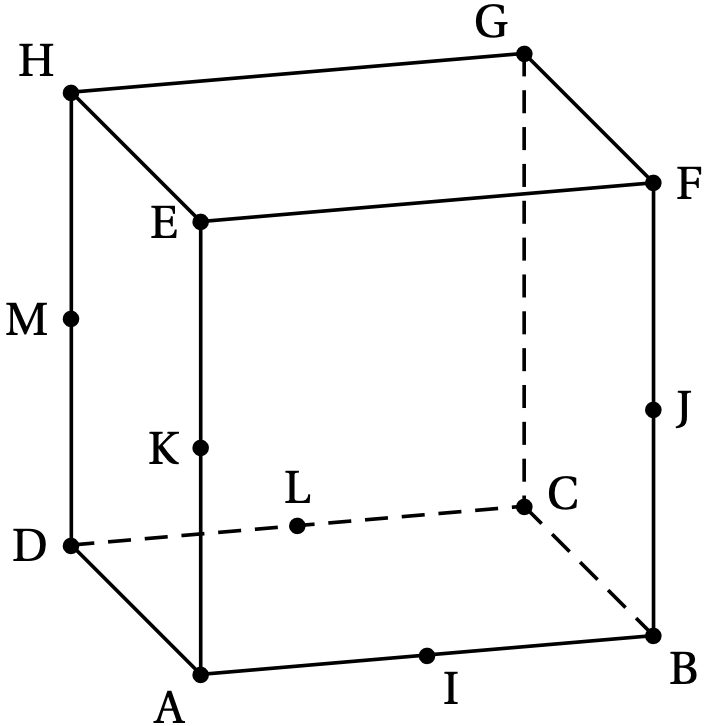
Affirmation 1 : « $\vec{\text{JH}} = 2\vec{\text{BI}} + \vec{\text{DM}} - \vec{\text{CB}}$ »
Affirmation 2 : « Le triplet de vecteurs $\left(\vec{\text{AB}},~\vec{\text{AH}},~\vec{\text{AG}}\right)$ est une base de l'espace. »
Affirmation 3 : « $\vec{\text{IB}} \cdot \vec{\text{LM}} = - \dfrac{1}{4}$. »
PARTIE B
Dans l'espace muni d'un repère orthonormé, on considère :
- le plan $\mathcal{P}$ d'équation cartésienne $2x - y + 3z + 6 = 0$
- les points A$(2~;~0~;~-1)$ et B$(5~;~-3~;~7)$
Affirmation 4 : « Le plan $\mathcal{P}$ et la droite (AB) sont parallèles. »
Affirmation 5 : « Le plan $\mathcal{P}'$ parallèle à $\mathcal{P}$ passant par B a pour équation cartésienne $-2x + y - 3z + 34 = 0$ »
Affirmation 6 : « La distance du point A au plan $\mathcal{P}$ est égale à $\dfrac{\sqrt{14}}{2}$. »
On note $(d)$ la droite de représentation paramétrique
$$\left\{\begin{array}{l c l} x &=&-12 + 2k\\ y &=&6\\ z &=&3 - 5k \end{array}\right., \text{où}\, k \in \mathbb{R}$$Affirmation 7 : « Les droites (AB) et $(d)$ ne sont pas coplanaires. »
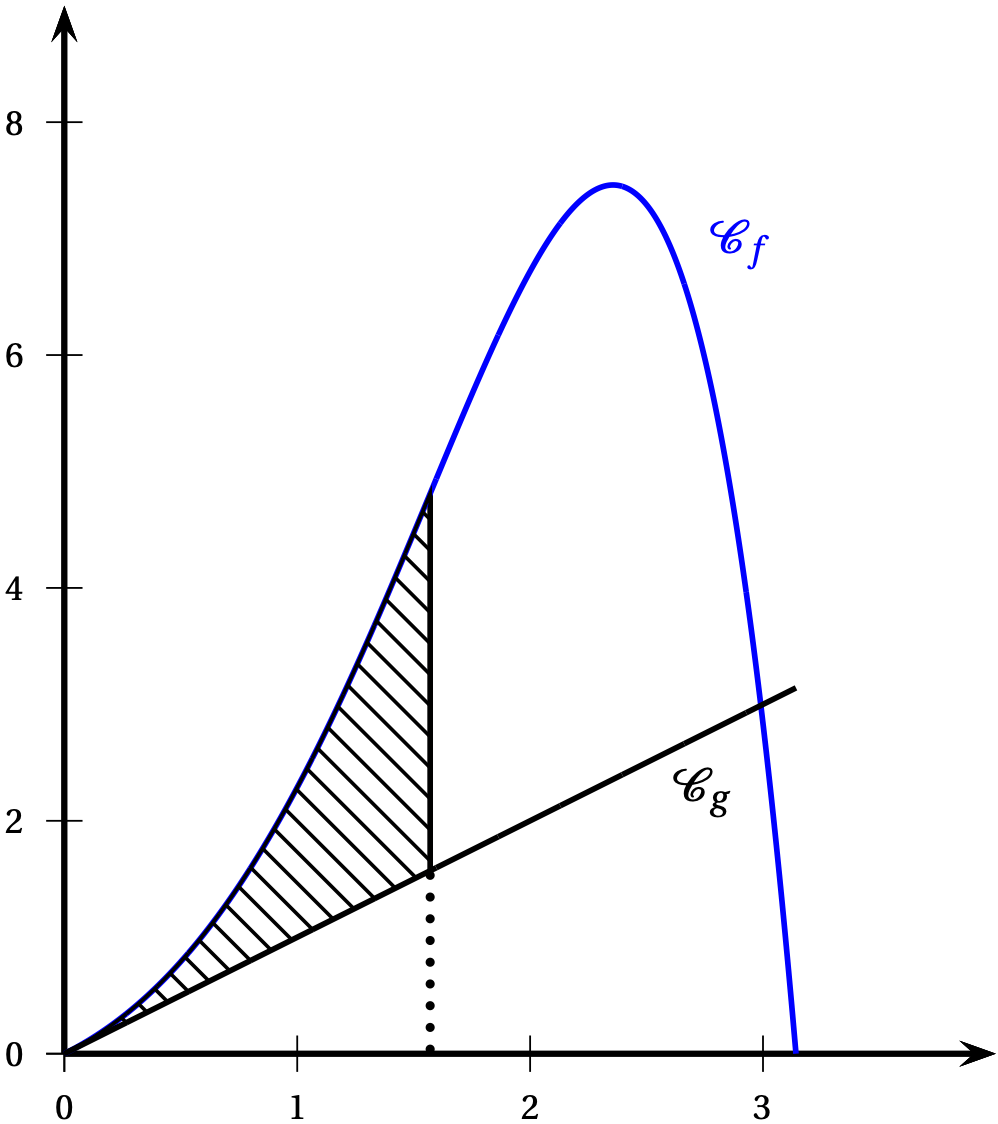
On désigne par $f$ la fonction définie sur l'intervalle $[0~;~\pi]$ par
$$f(x) = \mathrm{e}^x \sin (x).$$On note $\mathcal{C}_f$ la courbe représentative de $f$ dans un repère.
PARTIE A
-
- Démontrer que pour tout réel $x$ de l'intervalle $[0~;~\pi]$, $$f'(x) = \mathrm{e}^x[\sin(x) + \cos(x)].$$
- Justifier que la fonction $f$ est strictement croissante sur l'intervalle $\left[0~;~\dfrac{\pi}{2}\right]$
-
- Déterminer une équation de la tangente $T$ à la courbe $\mathcal{C}_f$ au point d'abscisse $0$.
- Démontrer que la fonction $f$ est convexe sur l'intervalle $\left[0~;~\dfrac{\pi}{2}\right]$.
- En déduire que pour tout réel $x$ de l'intervalle $\left[0~;~\dfrac{\pi}{2}\right]$, $\mathrm{e}^x \sin (x) \geqslant x$.
- Justifier que le point d'abscisse $\dfrac{\pi}{2}$ de la courbe représentative de la fonction $f$ est un point d'inflexion.
PARTIE B
On note
- En intégrant par parties l'intégrale $I$ de deux manières différentes, établir les deux relations suivantes : $$I= 1+J \qquad \text{et}\qquad I= \mathrm{e}^{\frac{\pi}{2}} - J.$$
- En déduire que $I = \dfrac{1 + \mathrm{e}^{\frac{\pi}{2}}}{2}$.
- On note $g$ la fonction définie sur $\mathbb{R}$ par $g(x) = x$.
Les courbes représentatives des fonctions $f$ et $g$ sont tracées dans le repère orthogonal ci-dessous sur l'intervalle $[0~;~\pi]$.
Calculer la valeur exacte de l'aire du domaine hachuré situé entre les courbes $\mathcal{C}_f$ et $\mathcal{C}_g$ et les droites d'équation $x = 0$ et $x = \dfrac{\pi}{2}$.
Contenu Premium
Cette vidéo explicative fait partie de notre contenu premium. Abonnez-vous pour accéder à toutes les méthodes détaillées.
Avec l'abonnement premium :
- Vidéos explicatives détaillées
- Accès à toutes les méthodes
- Exercices corrigés inclus
- Support prioritaire