Sujets de Bac
2025
Géométrie dans l'espace: partie 2
Filtrer par chapitre
Amerique Du Nord 21 Mai 2025 Jour 1
1 exercice
Pour chacune des affirmations suivantes, indiquer si elle est vraie ou fausse. Chaque réponse doit être justifiée. Une réponse non justifiée ne rapporte aucun point.
L'espace est rapporté à un repère orthonormé $(O;\vec{i},\vec{j},\vec{k})$.
On considère la droite $(d)$ dont une représentation paramétrique est :
$$\left\{\begin{array}{l c l} x&=&3 - 2 t \\ y&=&-1 \\ z&=&2 - 6 t \end{array} \quad, \text{ où } t \in \mathbb{R}\right.$$On considère également les points suivants :
- A$(3~;~-3~;~-2)$
- B$(5~;~-4~;~-1)$
- C le point de la droite $(d)$ d'abscisse 2
- H le projeté orthogonal du point B sur le plan $\mathcal{P}$ d'équation $x + 3z -7 = 0$
Affirmation 1
La droite $(d)$ et l'axe des ordonnées sont deux droites non coplanaires.
Affirmation 2
Le plan passant par $A$ et orthogonal à la droite $(d)$ a pour équation cartésienne :
$$x + 3z + 3= 0$$Affirmation 3
Une mesure, exprimée en radian, de l'angle géométrique $\widehat{\mathrm{BAC}}$ est $\dfrac{\pi}{6}$.
Affirmation 4
La distance BH est égale à $\dfrac{\sqrt{10}}{2}$.
Amerique Du Nord 22 Mai 2025 Jour 2
1 exercice
Pour chacune des affirmations suivantes, indiquer si elle est vraie ou fausse. Chaque réponse doit être justifiée.
Une réponse non justifiée ne rapporte aucun point.
PARTIE A
ABCDEFGH est un cube d'arête de longueur 1.
Les points I, J, K, L et M sont les milieux respectifs des arêtes [AB], [BF], [AE], [CD] et [DH].
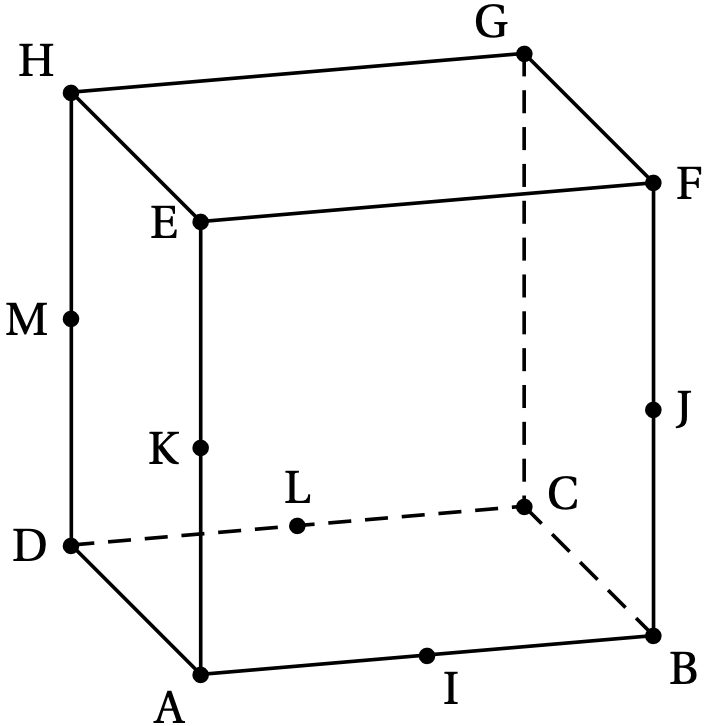
Affirmation 1 : « $\vec{\text{JH}} = 2\vec{\text{BI}} + \vec{\text{DM}} - \vec{\text{CB}}$ »
Affirmation 2 : « Le triplet de vecteurs $\left(\vec{\text{AB}},~\vec{\text{AH}},~\vec{\text{AG}}\right)$ est une base de l'espace. »
Affirmation 3 : « $\vec{\text{IB}} \cdot \vec{\text{LM}} = - \dfrac{1}{4}$. »
PARTIE B
Dans l'espace muni d'un repère orthonormé, on considère :
- le plan $\mathcal{P}$ d'équation cartésienne $2x - y + 3z + 6 = 0$
- les points A$(2~;~0~;~-1)$ et B$(5~;~-3~;~7)$
Affirmation 4 : « Le plan $\mathcal{P}$ et la droite (AB) sont parallèles. »
Affirmation 5 : « Le plan $\mathcal{P}'$ parallèle à $\mathcal{P}$ passant par B a pour équation cartésienne $-2x + y - 3z + 34 = 0$ »
Affirmation 6 : « La distance du point A au plan $\mathcal{P}$ est égale à $\dfrac{\sqrt{14}}{2}$. »
On note $(d)$ la droite de représentation paramétrique
$$\left\{\begin{array}{l c l} x &=&-12 + 2k\\ y &=&6\\ z &=&3 - 5k \end{array}\right., \text{où}\, k \in \mathbb{R}$$Affirmation 7 : « Les droites (AB) et $(d)$ ne sont pas coplanaires. »
Contenu Premium
Cette vidéo explicative fait partie de notre contenu premium. Abonnez-vous pour accéder à toutes les méthodes détaillées.
Avec l'abonnement premium :
- Vidéos explicatives détaillées
- Accès à toutes les méthodes
- Exercices corrigés inclus
- Support prioritaire