Sujets de Bac
2025
Fonctions logarithmes
Filtrer par chapitre
Tous les chapitres
Logique et raisonnements
Suites et Limites
Géométrie dans l'espace: partie 1
Limites de fonctions
Combinatoire et dénombrement
Continuité
Loi binomiale
Dérivation et convexité
Géométrie dans l'espace: partie 2
Fonctions logarithmes
Somme de variables aléatoires
Primitives et équations différentielles
Calcul intégral
Loi des grands nombres
Amerique Du Nord 22 Mai 2025 Jour 2
1 exercice
Exercice 1 - Amérique du Nord 22 mai 2025 J2
Un des objectifs de cet exercice est de déterminer une approximation du nombre réel $\ln(2)$, en utilisant une des méthodes du mathématicien anglais Henry Briggs au XVIe siècle.
On désigne par $(u_{n})$ la suite définie par :
$u_{0}=2$ et, pour tout entier naturel $n$, $u_{n+1}=\sqrt{u_{n}}$
Partie A
-
- Donner la valeur exacte de $u_{1}$ et de $u_{2}$.
- Émettre une conjecture, à l'aide de la calculatrice, sur le sens de variation et la limite éventuelle de la suite.
-
- Montrer par récurrence que pour tout entier naturel $n$, $1 \leqslant u_{n+1} \leqslant u_{n}$.
- En déduire que la suite $(u_{n})$ est convergente.
- Résoudre dans l'intervalle $[0~;~+\infty[$ l'équation $\sqrt{x} =x$.
- Déterminer, en justifiant, la limite de la suite $(u_{n})$.
Partie B
On désigne par $(v_{n})$ la suite définie pour tout entier naturel $n$ par $v_{n}=\ln \left(u_{n}\right)$.
-
- Démontrer que la suite $(v_{n})$ est géométrique de raison $\dfrac{1}{2}$.
- Exprimer $v_{n}$ en fonction de $n$, pour tout entier naturel $n$.
- En déduire que, pour tout entier naturel $n$, $\ln (2)=2^{n} \ln \left(u_{n}\right)$.
- On a tracé ci-dessous dans un repère orthonormé la courbe $\mathscr{C}$ de la fonction ln et la tangente T à la courbe $\mathscr{C}$ au point d'abscisse 1.
Une équation de la droite T est $y = x - 1$.
Les points $\mathrm{A}_{0}$, $\mathrm{A}_{1}$, $\mathrm{A}_{2}$ ont pour abscisses respectives $u_{0}$, $u_{1}$ et $u_{2}$ et pour ordonnée 0.
On décide de prendre $x - 1$ comme approximation de $\ln (x)$ lorsque $x$ appartient à l'intervalle $]0,99~;~1,01[$.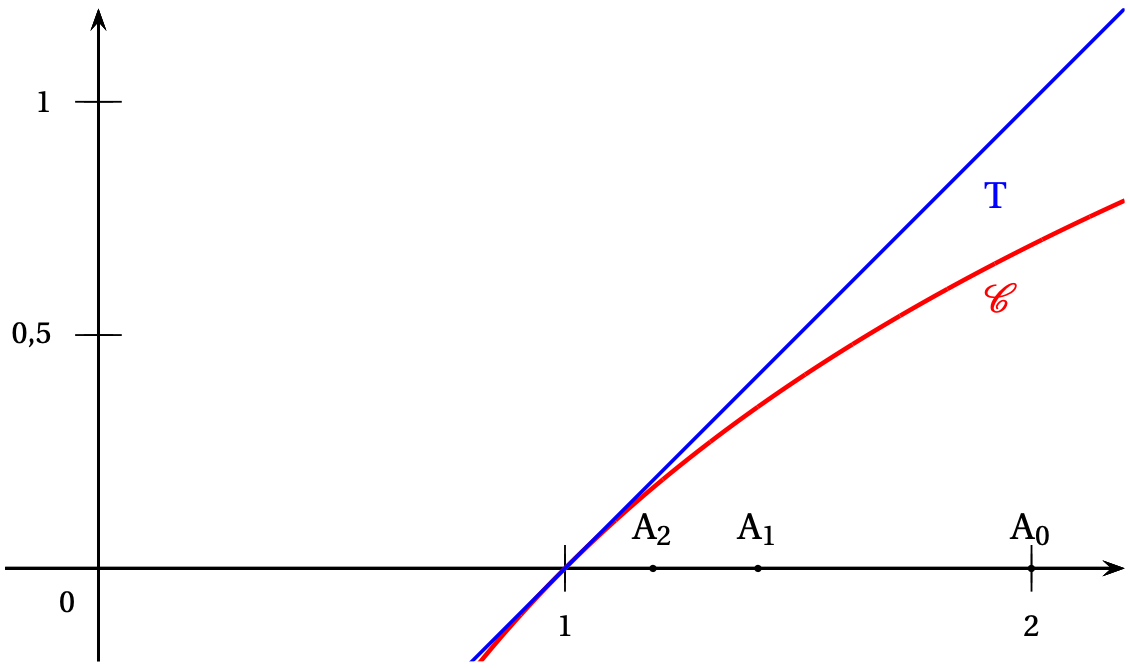
- Déterminer à l'aide de la calculatrice le plus petit entier naturel $k$ tel que $u_{k}$ appartienne à l'intervalle $]0,99 ~;~1,01[$ et donner une valeur approchée de $u_{k}$ à $10^{-5}$ près.
- En déduire une approximation de $\ln \left(u_{k}\right)$.
- Déduire des questions 1. c. et 2. b. de la partie B une approximation de $\ln (2)$.
- On généralise la méthode précédente à tout réel $a$ strictement supérieur à 1.
Recopier et compléter l'algorithme ci-dessous afin que l'appel Briggs(a) renvoie une approximation de $\ln (a)$.
On rappelle que l'instruction en langage Python sqrt(a) correspond à $\sqrt{a}$.from math import* def Briggs(a): n = 0 while a >= 1.01: a = sqrt(a) n = n+1 L =... return L
Contenu Premium
Cette vidéo explicative fait partie de notre contenu premium. Abonnez-vous pour accéder à toutes les méthodes détaillées.
Avec l'abonnement premium :
- Vidéos explicatives détaillées
- Accès à toutes les méthodes
- Exercices corrigés inclus
- Support prioritaire