Sujets de Bac
2025
Dérivation et convexité
Filtrer par chapitre
Tous les chapitres
Logique et raisonnements
Suites et Limites
Géométrie dans l'espace: partie 1
Limites de fonctions
Combinatoire et dénombrement
Continuité
Loi binomiale
Dérivation et convexité
Géométrie dans l'espace: partie 2
Fonctions logarithmes
Somme de variables aléatoires
Primitives et équations différentielles
Calcul intégral
Loi des grands nombres
Amerique Du Nord 21 Mai 2025 Jour 1
1 exercice
Exercice 1 - Amérique du Nord 21 mai 2025 J1
La partie C est indépendante des parties A et B.
Partie A
On donne ci-dessous, dans un repère orthogonal, les courbes $\mathcal{C}_{1}$ et $\mathcal{C}_{2}$, représentations graphiques de deux fonctions définies et dérivables sur $\mathbb{R}$. L'une des deux fonctions représentées est la fonction dérivée de l'autre. On les notera $g$ et $g'$.
On précise également que :
- La courbe $\mathcal{C}_{1}$ coupe l'axe des ordonnées au point de coordonnées $(0~;~1)$.
- La courbe $\mathcal{C}_{2}$ coupe l'axe des ordonnées au point de coordonnées $(0~;~2)$ et l'axe des abscisses aux points de coordonnées $(-2~;~0)$ et $(1~;~0)$.
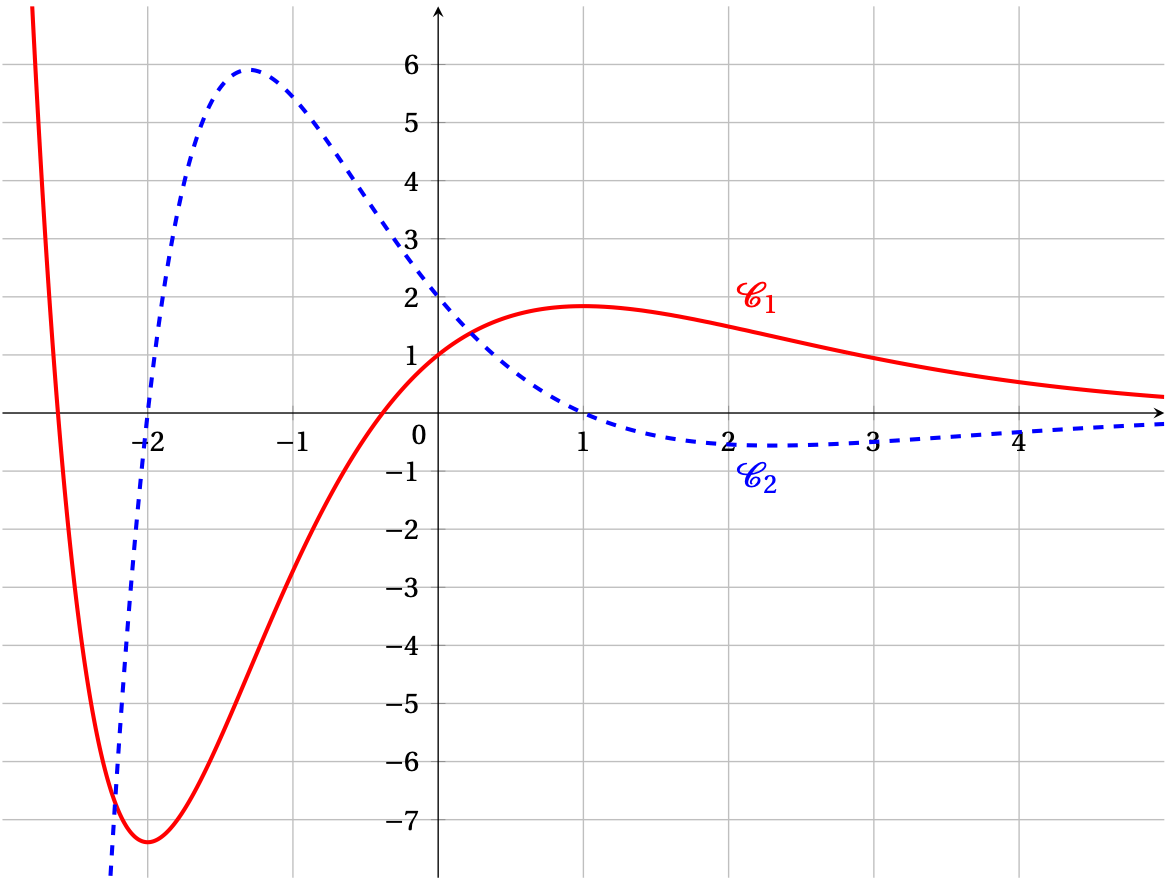
- En justifiant, associer à chacune des fonctions $g$ et $g'$ sa représentation graphique.
- Justifier que l'équation réduite de la tangente à la courbe représentative de la fonction $g$ au point d'abscisse 0 est $y=2x + 1$.
Partie B
On considère $(E)$ l'équation différentielle
$$y+y'=(2x + 3) \mathrm{e}^{-x},$$où $y$ est une fonction de la variable réelle $x$.
- Montrer que la fonction $f_{0}$ définie pour tout nombre réel $x$ par $f_{0}(x)=\left(x^{2}+3 x\right) \mathrm{e}^{-x}$ est une solution particulière de l'équation différentielle $(E)$.
- Résoudre l'équation différentielle $\left(E_{0}\right): y+ y'= 0$.
- Déterminer les solutions de l'équation différentielle $(E)$.
- On admet que la fonction $g$ décrite dans la partie A est une solution de l'équation différentielle $(E)$.
Déterminer alors l'expression de la fonction $g$. - Déterminer les solutions de l'équation différentielle $(E)$ dont la courbe admet exactement deux points d'inflexion.
Partie C
On considère la fonction $f$ définie pour tout nombre réel $x$ par :
$$f(x)=\left(x^{2}+3 x+2\right) \mathrm{e}^{-x}$$- Démontrer que la limite de la fonction $f$ en $+\infty$ est égale à 0.
On admet par ailleurs que la limite de la fonction $f$ en $-\infty$ est égale à $+\infty$. - On admet que la fonction $f$ est dérivable sur $\mathbb{R}$. On note $f'$ la fonction dérivée de $f$ sur $\mathbb{R}$.
- Vérifier que, pour tout nombre réel $x$, $f'(x)=\left(-x^{2}-x+1\right) \mathrm{e}^{-x}$.
- Déterminer le signe de la fonction dérivée $f'$ sur $\mathbb{R}$ puis en déduire les variations de la fonction $f$ sur $\mathbb{R}$.
- Expliquer pourquoi la fonction $f$ est positive sur l'intervalle $[0;+\infty[$.
- On notera $\mathcal{C}_{f}$ la courbe représentative de la fonction $f$ dans un repère orthogonal $(O;\vec{i},\vec{j})$. On admet que la fonction $F$ définie pour tout nombre réel $x$ par $F(x)=\left(-x^{2}-5 x-7\right) \mathrm{e}^{-x}$ est une primitive de la fonction $f$.
Soit $\alpha$ un nombre réel positif.
Déterminer l'aire $\mathcal{A}(\alpha)$, exprimée en unité d'aire, du domaine du plan délimité par l'axe des abscisses, la courbe $\mathcal{C}_{f}$ et les droites d'équation $x=0$ et $x=\alpha$.
Amerique Du Nord 22 Mai 2025 Jour 2
1 exercice
Exercice 1 - Amérique du Nord 22 mai 2025 J2
On désigne par $f$ la fonction définie sur l'intervalle $[0~;~\pi]$ par
$$f(x) = \mathrm{e}^x \sin (x).$$On note $\mathcal{C}_f$ la courbe représentative de $f$ dans un repère.
PARTIE A
-
- Démontrer que pour tout réel $x$ de l'intervalle $[0~;~\pi]$, $$f'(x) = \mathrm{e}^x[\sin(x) + \cos(x)].$$
- Justifier que la fonction $f$ est strictement croissante sur l'intervalle $\left[0~;~\dfrac{\pi}{2}\right]$
-
- Déterminer une équation de la tangente $T$ à la courbe $\mathcal{C}_f$ au point d'abscisse $0$.
- Démontrer que la fonction $f$ est convexe sur l'intervalle $\left[0~;~\dfrac{\pi}{2}\right]$.
- En déduire que pour tout réel $x$ de l'intervalle $\left[0~;~\dfrac{\pi}{2}\right]$, $\mathrm{e}^x \sin (x) \geqslant x$.
- Justifier que le point d'abscisse $\dfrac{\pi}{2}$ de la courbe représentative de la fonction $f$ est un point d'inflexion.
PARTIE B
On note
$I = \displaystyle\int_0^{\frac{\pi}{2}} \mathrm{e}^x \sin (x)\, \text{d}x$ et $J = \displaystyle\int_0^{\frac{\pi}{2}} \mathrm{e}^x \cos (x)\, \text{d}x.$
- En intégrant par parties l'intégrale $I$ de deux manières différentes, établir les deux relations suivantes : $$I= 1+J \qquad \text{et}\qquad I= \mathrm{e}^{\frac{\pi}{2}} - J.$$
- En déduire que $I = \dfrac{1 + \mathrm{e}^{\frac{\pi}{2}}}{2}$.
- On note $g$ la fonction définie sur $\mathbb{R}$ par $g(x) = x$.
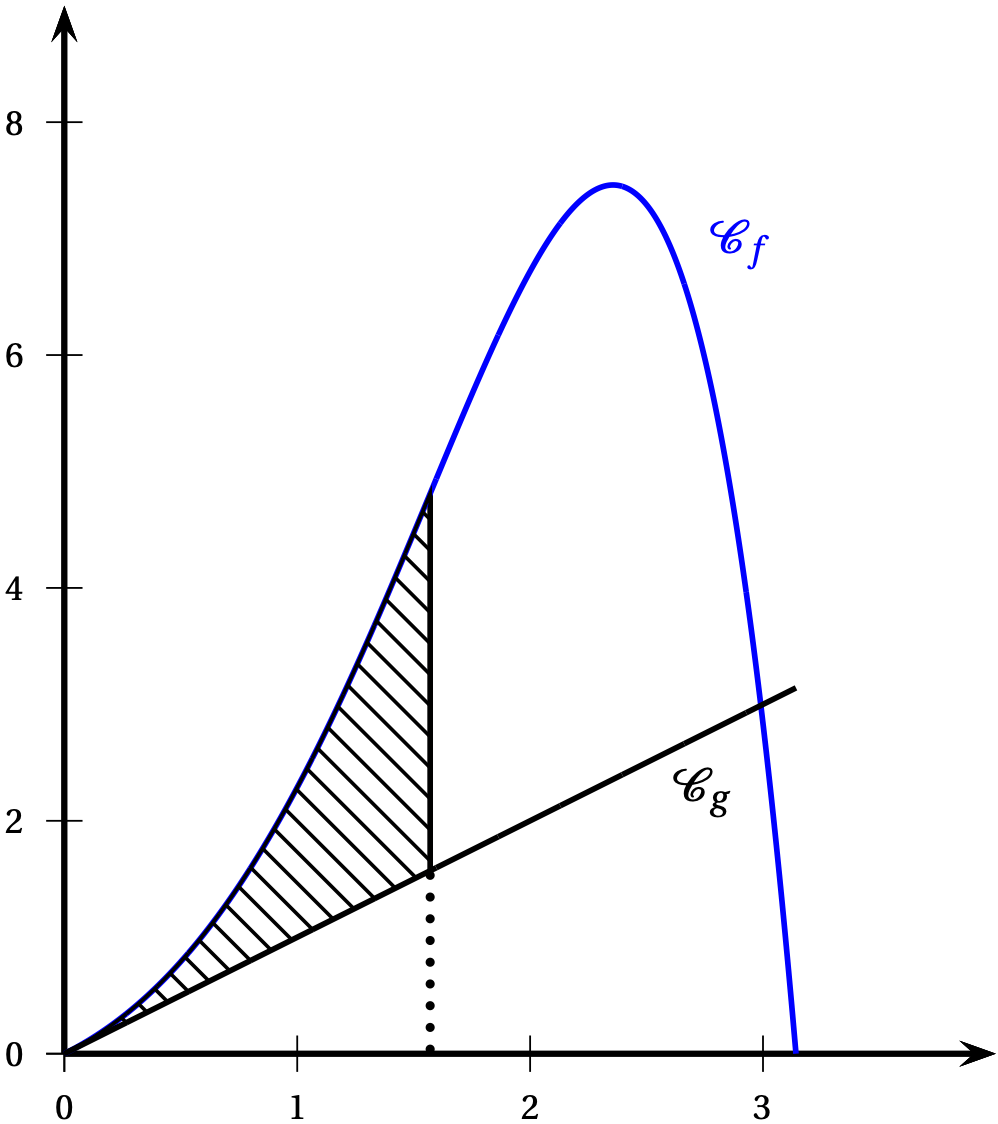
Les courbes représentatives des fonctions $f$ et $g$ sont tracées dans le repère orthogonal ci-dessous sur l'intervalle $[0~;~\pi]$.
Calculer la valeur exacte de l'aire du domaine hachuré situé entre les courbes $\mathcal{C}_f$ et $\mathcal{C}_g$ et les droites d'équation $x = 0$ et $x = \dfrac{\pi}{2}$.
Contenu Premium
Cette vidéo explicative fait partie de notre contenu premium. Abonnez-vous pour accéder à toutes les méthodes détaillées.
Avec l'abonnement premium :
- Vidéos explicatives détaillées
- Accès à toutes les méthodes
- Exercices corrigés inclus
- Support prioritaire