Les exercices
sur 6 exercices complétés
Simplifier les expressions suivantes
- $cos(\pi)+cos(\frac{-\pi}{2})+cos(\frac{\pi}{2})+cos(\frac{\pi}{3})$
- $sin(\frac{-\pi}{3})\times cos(\frac{3\pi}{4})-cos(\frac{7\pi}{3})\times sin(\frac{5\pi}{6})$
- $(sin(\frac{7\pi}{4}))^2 - cos(\frac{23\pi}{3})+sin(\frac{-15\pi}{6})$
- $cos(55\pi)\times sin(-\frac{44\pi}{3})+cos(\frac{13\pi}{4})\times sin(\frac{27\pi}{2})$
- Résoudre dans l'intervalle $[-\pi;\pi]$ les équations:
- $cos^2(x)=1$
- $2sin^2(x)-1=0$
- Résoudre dans l'intervalle $[0;2\pi]$ l'équation:
$2sin^2(x)+5sin(x)-3=0$
- Résoudre dans l'intervalle $[0;2\pi]$ l'équation:
$-sin^2(x)+2sin(x)+2=0$
Compléter le tableau suivant
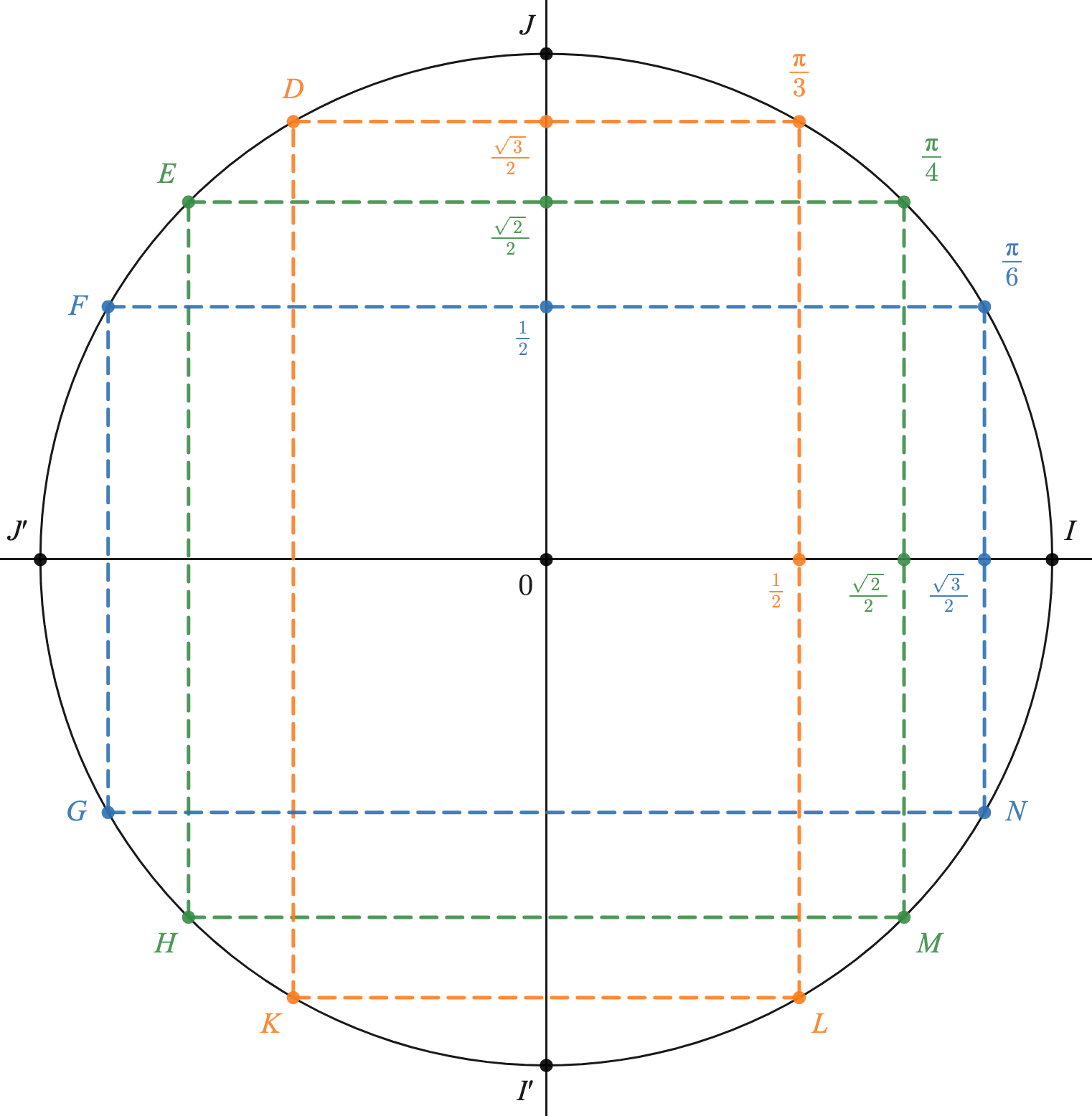
| $x$ | $\frac{-2\pi}{3}$ | $\frac{5\pi}{6}$ | $\frac{-\pi}{4}$ | $\frac{3\pi}{4}$ | $\frac{7\pi}{6}$ | $\frac{2\pi}{3}$ |
| Point Image |
||||||
| $cos(x)$ | ||||||
| $sin(x)$ |
Résoudre les équations suivantes
- $cos(x)=-\frac{\sqrt{3}}{2}$
- avec $x\in [-\pi;0]$
- avec $x\in [0;2\pi]$
- $sin(x)=\frac{\sqrt{2}}{2}$
- avec $x\in [\frac{\pi}{2};2\pi]$
- avec $x\in [-\pi;\pi]$
- $cos(x)=\frac{1}{2}$
- avec $x\in [\frac{\pi}{2};\frac{3\pi}{2}]$
- avec $x\in [\pi;3\pi]$
On considère le cercle trigonométrique ci-dessous qui contient une partie rouge et en pointillés la droite d'équation $x=\frac{1}{2}$
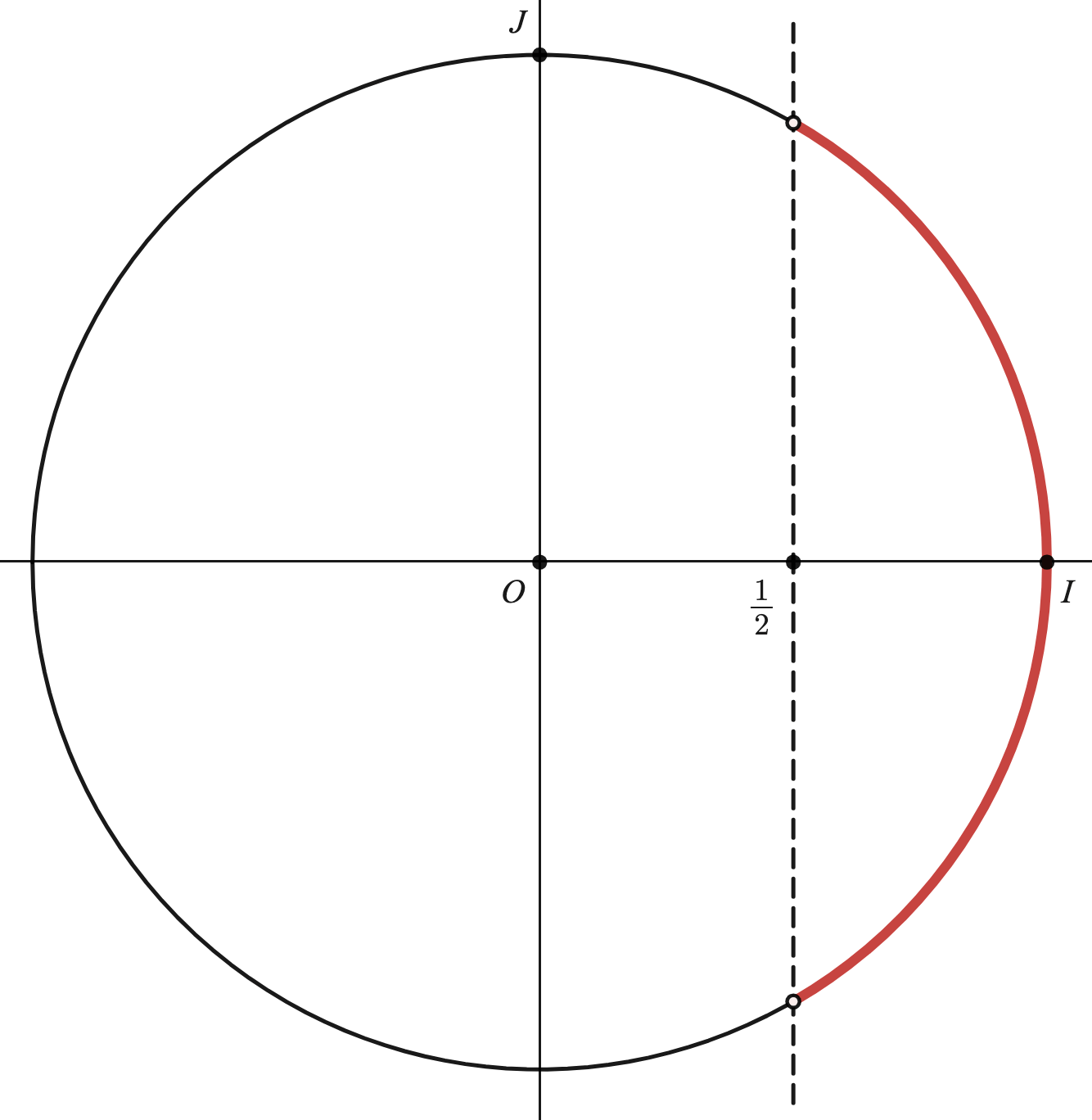
- Résoudre $cos(x)\geq \frac{1}{2}$ dans $[-\pi;\pi]$ grâce au schéma
- Résoudre les équations suivantes dans $[-\pi;\pi]$ en utilisant la même méthode
- $sin(x)>\frac{1}{2}$
- $cos(x)<-\frac{\sqrt{2}}{2}$
- $sin(x)\leq -\frac{\sqrt{3}}{2}$
La mesure principale d'un angle est la mesure de cet angle qui appartient à l'intervalle $[-\pi;\pi]$
- Donner la mesure principale des angles: $\dfrac{13\pi}{2}$, $\dfrac{-9\pi}{2}$, $\dfrac{23\pi}{3}$
- Décrire ce que fait l'agorithme suivant:

Contenu Premium
Cette vidéo explicative fait partie de notre contenu premium. Abonnez-vous pour accéder à toutes les méthodes détaillées.
Avec l'abonnement premium :
- Vidéos explicatives détaillées
- Accès à toutes les méthodes
- Exercices corrigés inclus
- Support prioritaire
Trigonométrie
Fiche de synthèse
Contenu Complet Premium
Pour accéder au contenu complet de cette fiche de cours, vous devez vous abonner à notre offre premium.
Avec l'abonnement premium :
- Fiches de cours complètes
- Accès à toutes les méthodes
- Exercices corrigés inclus
- Vidéos explicatives détaillées


