Calculer les 3 premiers termes des suites suivantes

1. $u_{n}=2n-5$
2. $v_{n}=3n^2+1$
3. $w_{n}=\dfrac{-4n+1}{n}$
4. $p_{n}=\sqrt{n+5}$

Calculer les 3 premiers termes des suites suivantes

1. $u_{0}=5$ et $u_{n+1}=2u_{n}-3$
2. $v_{0}=-1$ et $v_{n+1}=v_{n}(1-v_{n})$
3. $w_{0}=3$ et $w_{n+1}=2w_{n}-w_{n}^2+1$

Représenter graphiquement les 4 premiers termes des suites suivantes

1. $u_{n}=2n-3$
2. $v_{n}=n-n^2+2$
3. $w_{n+1}=2w_{n}-n+1$ et $w_{0}=1$
4. $t_{n+1}=t_{n}^2-t_{n}-3$ et $t_{0}=2$

Pour chacune des suites suivantes exprimer $u_{n+1}$ et $u_{n-1}$ en fonction de $n$

1. $u_{n}=-2n+5$
2. $v_{n}=\frac{2n+3}{n-1}$
3. $w_{n}=1-2n^2$
4. $t_{n}=\frac{2^n}{5^{n+1}}$

Donner la relation entre $u_{n+1}$ et $u_{n}$ sachant qu'à chaque étape

1. $u_{n}$ double
2. $u_{n}$ diminue de 6,5
3. $u_{n}$ diminue de 8%
4. $u_{n}$ triple et augmente de 7
5. $u_{n}$ augmente de 12% et baisse de 50

Utiliser le tableur pour exprimer les suites sous forme explicite ou par récurrence

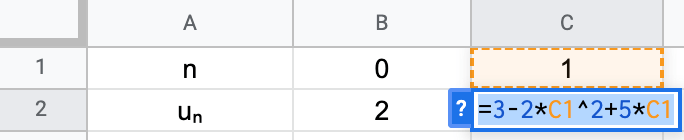
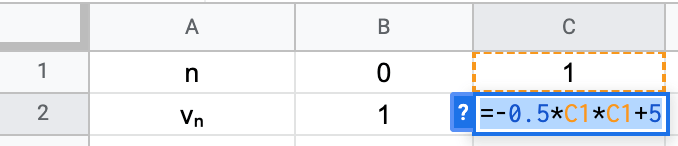
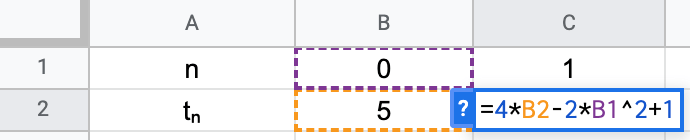
Pour les suites suivantes, indiquer la dernière valeur calculée lorsque la suite a une formule explicite et exprimer $u_{n}$ en fonction de $n$ ou $u_{n+1}$ en fonction de $u_{n}$

    Pour i allant de 1 à 8
      U ← 3i+2
    Fin Pour

    U ← 3
    Pour k allant de 1 à 4
      U ← (U-2)/(U+5)
    Fin Pour

    j=0
    while j < 12
      u = j(j-1)+3
      j = j+1

    u = 4
    for i in range(1,8)
      u = u**2+2*u+1
    print(u)