On considère le triangle $ABC$ ci-dessous.

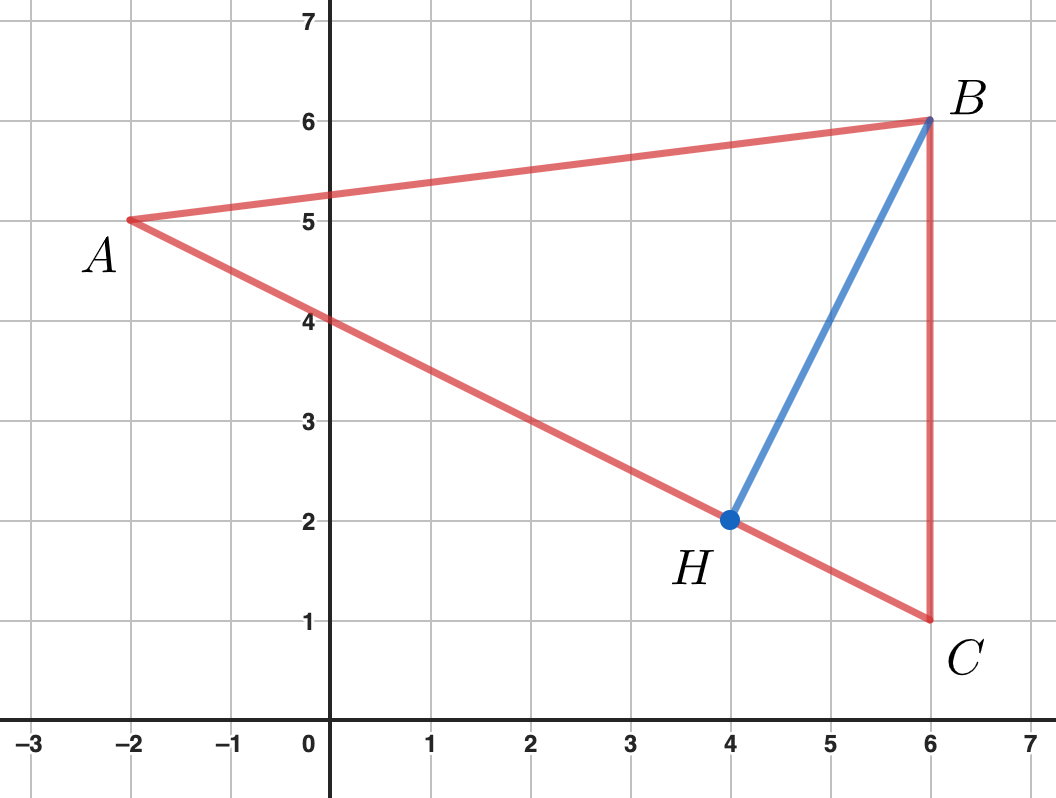
1. Démontrer que le point $H$ est le projeté orthogonal de $B$ sur $(AC)$.
2. En déduire l'aire du triangle $ABC$.

On considère le carré $EFGH$ ci-dessous. $J$ est le milieu de $[GH]$ et $I$ est le point de $[FG]$ tel que $GI=\dfrac{3}{4}FG$.

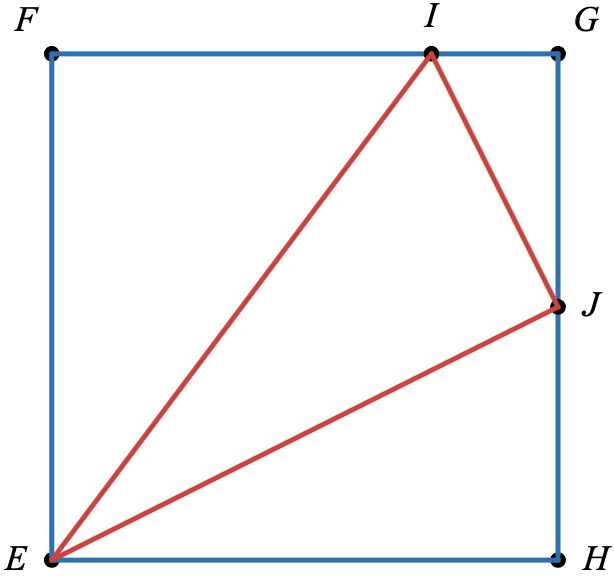
1. $(E;~\overrightarrow{EH};~\overrightarrow{EF})$ est-il un repère orthonormé? Justifier.
2. Déterminer les coordonnés des points dans le repère $(E;~\overrightarrow{EH};~\overrightarrow{EF})$.
3. Déterminer la nature du triangle $EIJ$.

On considère les points $M(-3;~2)$, $N(5;~-4)$, $P(6;~-1)$ et $Q(-4;~-2)$ et $C$ le cercle de diamètre de diamètre $[MN]$.

1. Déterminer les coordonnées du point $I$, milieu de $[MN]$.
2. Les points $P$ et $Q$ appartiennent-il au cercle?
3. Quelle est la nature du triangle $MNP$?
4. Soit $K(x;~y)$ un point quelconque du plan. Exprimer la distance $IK$ en fonction de $x$ et $y$.
5. En deduire l'équation du cercle de centre $I$ et de diamètre $[MN]$.
6. Utiliser l'équation précédente pour redémontrer les résultat de la question 2.

On considère le cercle de centre $O$ et de rayon $OA$. La droite $(AB)$ est tangente au cercle en $A$
$AB=21$, $BC=9$

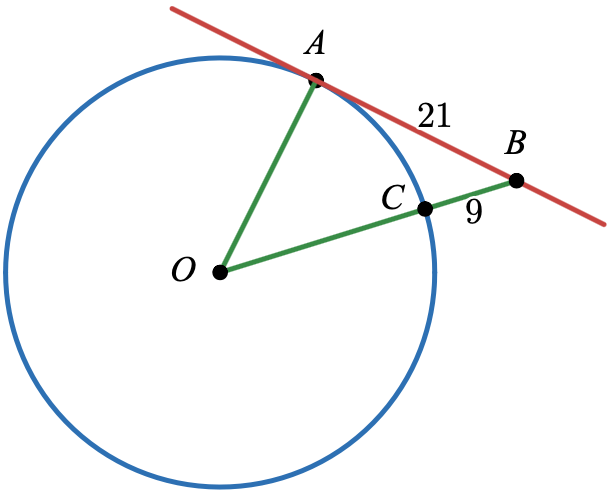
Déterminer la valeur du rayon du cercle.