Les exercices
sur 5 exercices complétés
Soit $f$ la fonction définie sur $\R$ par $f(x)=x^3$.
- Montrer que pour tous nombres réels $a$ et $b$, $(a+b)^3=a^3+3a^2b+3ab^2+b^3$.
- Calculer $\dfrac{f(3+h)-f(3)}{h}$.
- En déduire que $f$ est dérivable en $3$ et que $f'(3)=27$
- En utilisant un calcul similaire à celui de la question 2, prouver que $f'(x)=3x^2$ pour tout $x\in \R$.
Déterminer l'ensemble de définition et de dérivabilité des fonctions suivantes puis calculer la fonction dérivée.
- $f(x)=\dfrac{3x^2+2x+1}{6}$
- $g(x)=(1-3x^2)\sqrt{x}$
- $h(x)=\dfrac{2x^2-1}{x^2+x+1})$
- $k(x)=(7x-3)^4$
- $j(x)=\sqrt{4x+5}$
Soit $f$ la fonction de courbe représentative $C_f$ définie par:$$f(x)=\dfrac{x^2-1}{2x-1}$$
- Déterminer le domaine de définition $D_f$ et de dérivabilité $D_{f'}$ de la fonction $f$.
- Calculer $f'(x)$ pour tout $x\in D_{f'}$.
- Déterminer l'équation réduite de la tangente à $C_f$ au point d'abscisse $-1$.
- La courbe de la fonction admet-elle des tangentes horizontales? Si oui, pour quelle valeurs de $x$?
- On considère la droite $(d)$ d'équation $y=2x-\dfrac{7}{2}$. Déterminer les coordonnées des points de la courbe $C_f$ pour lesquels la tangente à $C_f$ est parallèle à $(d)$.
Soit $f$ la fonction définie par:$$f(x)=(x^3-2x+5)(2x^2+1)$$
- Déterminer le domaine de définition $D_f$ et de dérivabilité $D_{f'}$ de la fonction $f$.
- Calculer $f'(x)$ après avoir développé $f(x)$.
- Calculer $f'(x)$ en utilisant la formule de la dérivée d'un produit de fonctions.
- Déterminer l'équation réduite de la tangente à la courbe en $x=1$.
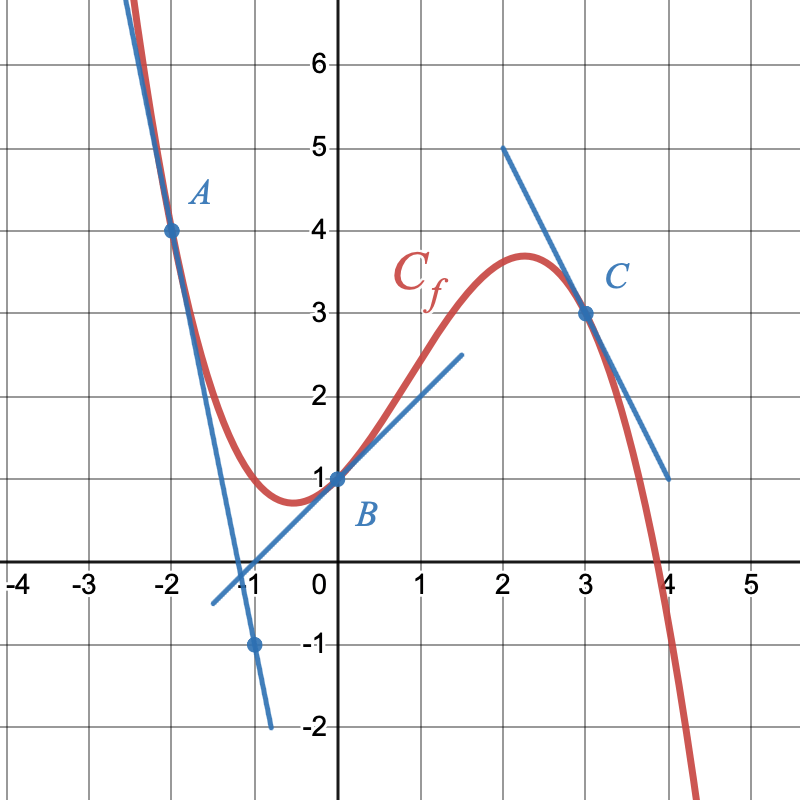
La figure ci-contre représente la courbe d'une fonction en rouge ainsi que ses tangentes au points $A$, $B$ et $C$.
- Déterminer graphiquement les valeurs de $f(0)$, $f(-2)$, $f(3)$ puis de $f'(-2)$, $f'(0)$ et $f'(3)$.
- Déterminer les équations des 3 tangentes représentées.
- Combien de tangentes horizontales cette fonction semble-t'elle avoir?
- Déterminer les coordonnées du point d'intersection des tangentes en $x=0$ et $x=3$.
Contenu Premium
Cette vidéo explicative fait partie de notre contenu premium. Abonnez-vous pour accéder à toutes les méthodes détaillées.
Avec l'abonnement premium :
- Vidéos explicatives détaillées
- Accès à toutes les méthodes
- Exercices corrigés inclus
- Support prioritaire
Dérivation partie 1
Fiche de synthèse
Logarithmes
La fonction réciproque de la fonction exponentielle $y=e^x$ s'appelle la fonction logarithme népèrien et est définie par: $$\begin{cases} x\mapsto ln(x) \newline ]0;~+\infin[ \to \R \end{cases}$$
Pour tout nombre $a>0$, la fonction logarithme népèrien de $a$ l'unique solution réelle de l'équation $e^x=a$
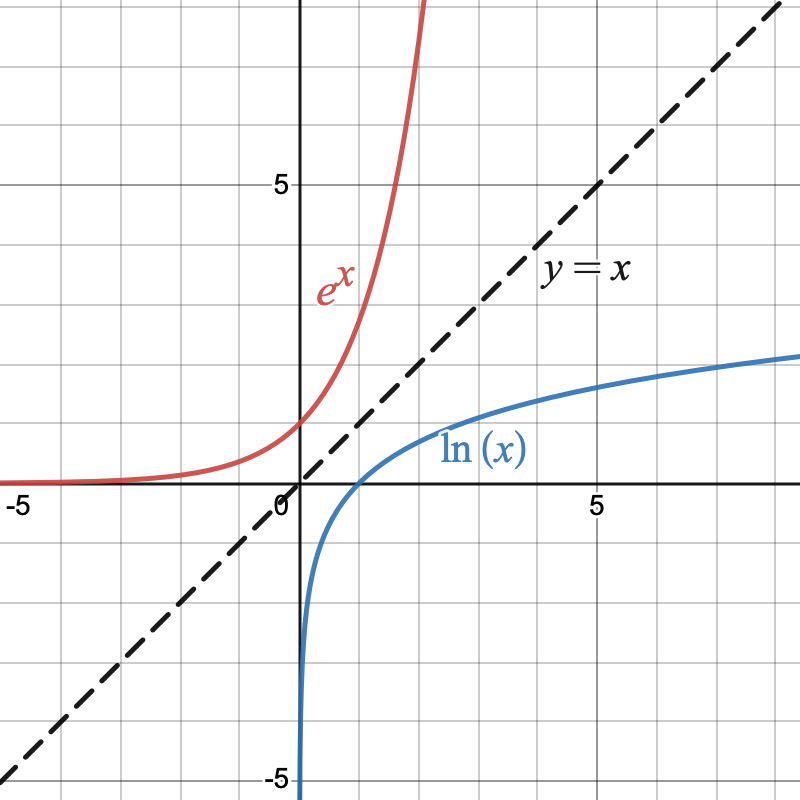
- Pour tout $x\in ]0;~+\infin[$, on a $e^{ln(x)}=x$
- Pour tout $x\in \R$, on a $ln(e^x)=x$
Contenu Complet Premium
Pour accéder au contenu complet de cette fiche de cours, vous devez vous abonner à notre offre premium.
Avec l'abonnement premium :
- Fiches de cours complètes
- Accès à toutes les méthodes
- Exercices corrigés inclus
- Vidéos explicatives détaillées


