Sujets de Bac
2024
Primitives et équations différentielles
Filtrer par chapitre
Asie 11 Juin 2024 Jour 2
1 exercice
Pour chacune des affirmations suivantes, indiquer si elle est vraie ou fausse. Chaque réponse doit être justifiée. Une réponse non justifiée ne rapporte aucun point.
-
Soit $ (u_n) $ une suite définie pour tout entier naturel $ n $ et vérifiant la relation suivante :
$$ \dfrac{1}{2} < u_n \leq \dfrac{3n^2 + 4n + 7}{6n^2 + 1} \text{ pour tout entier naturel } n $$.
Affirmation 1 : $ \lim\limits_{n \to +\infty} u_n = \dfrac{1}{2} $.
-
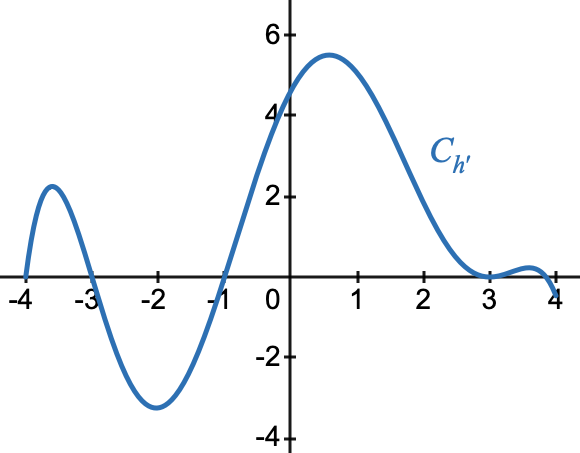
Soit $ h $ une fonction définie et dérivable sur l’intervalle $[-4 ; 4]$. La représentation graphique $ \mathcal{C}_{h'} $ de sa fonction dérivée $ h' $ est donnée ci-dessous.
Affirmation 2 : La fonction $ h $ est convexe sur $[-1 ; 3]$.
-
Le code d’un immeuble est composé de 4 chiffres (qui peuvent être identiques) suivis de deux lettres distinctes parmi A, B et C (exemple : 1232BA).
Affirmation 3 : Il existe 20 634 codes qui contiennent au moins un 0.
-
On considère la fonction $ f $ définie sur $ \left] 0 ; +\infty \right[ $ par $ f(x) = x \ln x $.
Affirmation 4 : La fonction $ f $ est une solution sur $ \left] 0 ; +\infty \right[ $ de l’équation différentielle
$$ x y' - y = x $$.
Centres Etrangers 5 Juin 2024 Jour 1
1 exercice
On considère l’équation différentielle $$(E_0) : y' = y $$ où $ y $ est une fonction dérivable de la variable réelle $ x $.
- Démontrer que l’unique fonction constante solution de l’équation différentielle $ (E_0) $ est la fonction nulle.
- Déterminer toutes les solutions de l’équation différentielle $ (E_0) $.
- La fonction $ h $ est définie sur $ \mathbb{R} $ par $ h(x) = 2 \cos(x) + \sin(x) $.
On admet qu’elle est dérivable sur $ \mathbb{R} $.
Démontrer que la fonction $ h $ est solution de l’équation différentielle $ (E) $. - On considère une fonction $ f $ définie et dérivable sur $ \mathbb{R} $.
Démontrer que : « $ f $ est solution de $ (E) $ » est équivalent à « $ f - h $ est solution de $(E_0)$ ». - En déduire toutes les solutions de l’équation différentielle $ (E) $.
- Déterminer l’unique solution $ g $ de l’équation différentielle $ (E) $ telle que $ g(0) = 0 $.
- Calculer : $$ \int_{0}^{\frac{\pi}{2}} \left[-2e^x + \sin(x) + 2 \cos(x)\right] \mathrm{d}x. $$
On considère l’équation différentielle $$ (E) : y' = y - \cos(x) - 3 \sin(x) $$ où $ y $ est une fonction dérivable de la variable réelle $ x $.
Metropole 19 Juin 2024 Jour 1
1 exercice
Pour chacune des affirmations suivantes, indiquer si elle est vraie ou fausse. Chaque réponse doit être justifiée. Une réponse non justifiée ne rapporte aucun point.
-
On considère la fonction $f$ définie sur $\mathbb{R}$ par : $f(x)=5x\mathrm{e}^{-x}$.
On note $C_f$ la courbe représentative de $f$ dans un repère orthonormé.Affirmation 1 :
L'axe des abscisses est une asymptote horizontale à la courbe $C_f$.
Affirmation 2 :
La fonction $f$ est solution sur $\mathbb{R}$ de l'équation différentielle $(E)$ : $y' + y = 5\mathrm{e}^{-x}$.
-
On considère les suites $\left(u_n\right)$, $\left(v_n\right)$ et $\left(w_n\right)$, telles que, pour tout entier naturel $n$ : $$ u_n \leqslant v_n \leqslant w_n. $$
De plus, la suite $\left(u_n\right)$ converge vers $-1$ et la suite $\left(w_n\right)$ converge vers $1$.
Affirmation 3 :
La suite $\left(v_n\right)$ converge vers un nombre réel $\ell$ appartenant à l'intervalle $[-1; 1]$.
On suppose de plus que la suite $\left(u_n\right)$ est croissante et que la suite $\left(w_n\right)$ est décroissante.
Affirmation 4 :
Pour tout entier naturel $n$, on a alors : $u_0 \leqslant v_n \leqslant w_0$.
Metropole 20 Juin 2024 Jour 2
1 exercice
Les parties A et B sont indépendantes
Alain possède une piscine qui contient $50 ~\mathrm{m}^{3}$ d'eau. On rappelle que $1 ~\mathrm{m}^{3} = 1000 \mathrm{L}$.
Pour désinfecter l'eau, il doit ajouter du chlore.
Le taux de chlore dans l'eau, exprimé en $ \mathrm{mg} \cdot \mathrm{L}^{-1} $, est défini comme la masse de chlore par unité de volume d'eau. Les piscinistes préconisent un taux de chlore compris entre $1$ et $3~\mathrm{mg \cdot L}^{-1}$.
Sous l'action du milieu ambiant, notamment des ultraviolets, le chlore se décompose et disparaît peu à peu.
Alain réalise certains jours, à heure fixe, des mesures avec un appareil qui permet une précision à $0,01 ~\mathrm{mg \cdot L}^{-1}$. Le mercredi 19 juin, il mesure un taux de chlore de $0,70 ~\mathrm{mg \cdot L}^{-1}$.
Partie A : étude d'un modèle discret.
- Justifier que cet ajout de chlore fait augmenter le taux de $0,3, \mathrm{mg \cdot L}^{-1}$.
-
- Pour tout entier naturel $n$, on note $v_{n}$ le taux de chlore, en $ \mathrm{mg \cdot L}^{-1} $, obtenu avec ce nouveau protocole $n$ jours après le mercredi 19 juin. Ainsi $v_{0}=0,7$.
On admet que pour tout entier naturel $n$, $$ v_{n+1}=0,92 v_{n}+ 0,3. $$ - Montrer par récurrence que pour tout entier naturel $n$, $$ v_{n} \leqslant v_{n+1} \leqslant 4. $$
- Montrer que la suite $ (v_{n}) $ est convergente et calculer sa limite.
- Pour tout entier naturel $n$, on note $v_{n}$ le taux de chlore, en $ \mathrm{mg \cdot L}^{-1} $, obtenu avec ce nouveau protocole $n$ jours après le mercredi 19 juin. Ainsi $v_{0}=0,7$.
- À long terme, le taux de chlore sera-t-il conforme à la préconisation des piscinistes ? Justifier la réponse.
- Reproduire et compléter l'algorithme ci-après écrit en langage Python pour que la fonction
alerte_chlorerenvoie, lorsqu'il existe, le plus petit entier $n$ tel que $v_{n}> s$. - Quelle valeur obtient-on en saisissant l'instruction
alerte_chlore(3)? Interpréter ce résultat dans le contexte de l'exercice.
def alerte_chlore(s):
n = 0
u = 0.7
while ...:
n = ...
u = ...
return n
Partie B : étude d'un modèle continu.
Alain décide de faire appel à un bureau d'études spécialisées. Celui-ci utilise un modèle continu pour décrire le taux de chlore dans la piscine.
Dans ce modèle, pour une durée $x$ (en jours écoulés à compter du mercredi 19 juin), $f(x)$ représente le taux de chlore, en $ \mathrm{mg} \cdot \mathrm{L}^{-1} $, dans la piscine.
On admet que la fonction $f$ est solution de l'équation différentielle $(E)$ : $$ y'=-0,08 y+\frac{q}{50}, $$ où $q$ est la quantité de chlore, en grammes, rajoutée dans la piscine chaque jour.
- Justifier que la fonction $f$ est de la forme : $$ f(x)=C e^{-0,08 x}+\frac{q}{4}, $$ où $C$ est une constante réelle.
-
- Exprimer en fonction de $q$ la limite de $f$ en $+\infty$.
- On rappelle que le taux de chlore observé le mercredi 19 juin est égal à $0,7~\mathrm{mg \cdot L}^{-1}$.
On souhaite que le taux de chlore se stabilise à long terme autour de $2~\mathrm{mg \cdot L}^{-1}$. Déterminer les valeurs de $C$ et $q$ afin que ces deux conditions soient respectées.
Polynesie 19 Juin 2024 Jour 1
1 exercice
Une entreprise fabrique des objets en plastique en injectant dans un moule de la matière fondue à $210$~°C. On cherche à modéliser le refroidissement du matériau à l'aide d'une fonction $f$ donnant la température du matériau injecté en fonction du temps $t$.
Le temps est exprimé en secondes et la température est exprimée en degré Celsius.
On admet que la fonction $f$ cherchée est solution d'une équation différentielle de la forme suivante où $m$ est une constante réelle que l'on cherche à déterminer :
$$ (E) : ~ y' +0,02y = m. $$
Partie A
- Justifier l'affichage suivant d'un logiciel de calcul formel :
Entrée : RésoudreEquationDifférentielle $(y' + 0,02y = m)$ Sortie : $\to y = k \cdot \exp(-0.02 \cdot t) + 50 \cdot m$ - La température de l'atelier est de $30$°C. On admet que la température $f(t)$ tend vers $30$°C lorsque $t$ tend vers l'infini.
Démontrer que $m = 0,6$. - Déterminer l'expression de la fonction $f$ cherchée en tenant compte de la condition initiale $f(0) = 210$.
Partie B
On admet ici que la température (exprimée en degré Celsius) du matériau injecté en fonction du temps (exprimé en seconde) est donnée par la fonction dont l'expression et une représentation graphique sont données ci-dessous :
$$ f(t) =180 e^{-0,02t} + 30. $$
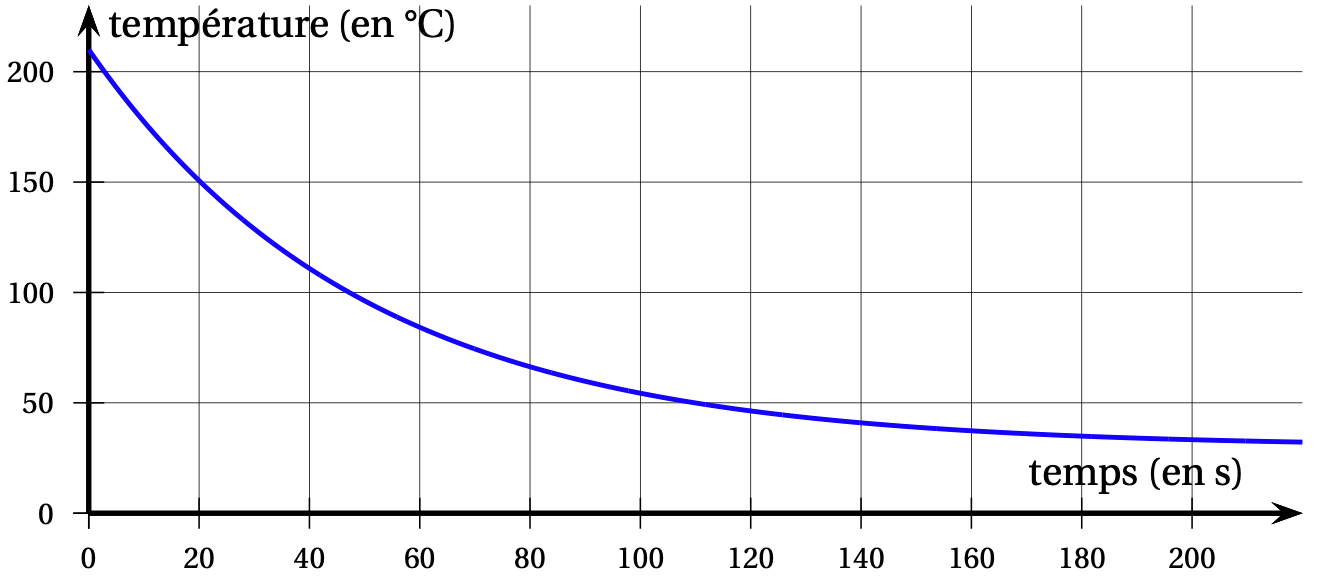
- L'objet peut être démoulé lorsque sa température devient inférieure à $50$°C.
- Par lecture graphique, donner une valeur approchée du nombre $T$ de secondes à attendre avant de démouler l'objet.
- Déterminer par le calcul la valeur exacte de ce temps $T$.
- À l'aide d'une intégrale, calculer la valeur moyenne de la température sur les $100$ premières secondes.
Polynesie 20 Juin 2024 Jour 2
1 exercice
Cet exercice est un questionnaire à choix multiples (QCM) qui comprend cinq questions. Les cinq questions sont indépendantes.
Pour chacune des questions, une seule des quatre réponses est exacte. Le candidat indiquera sur sa copie le numéro de la question suivi de la lettre correspondant à la réponse exacte.
Aucune justification n'est demandée.
Une réponse fausse, une réponse multiple ou une absence de réponse ne rapporte, ni n'enlève aucun point.
- La solution $ f $ de l'équation différentielle $ y'=-3y+7 $ telle que $ f(0)=1 $ est la fonction définie sur $ \mathbb{R} $ par :
- $ f(x) = e^{-3x} $
- $ f(x) = - \dfrac{4}{3} e^{-3x} + \dfrac{7}{3} $
- $ f(x) = e^{-3x} + \dfrac{7}{3} $
- $ f(x) = - \dfrac{10}{3} e^{-3x} - \dfrac{7}{3} $
-
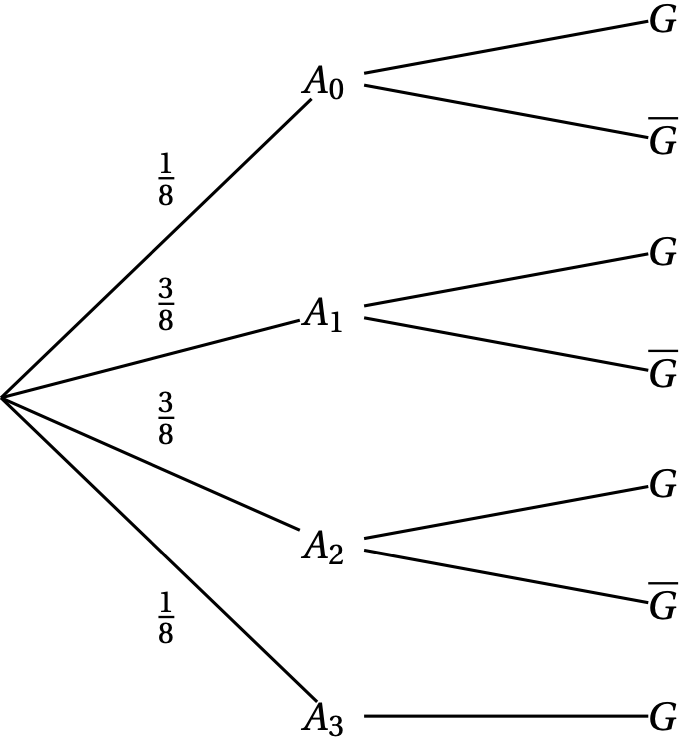
- On considère la fonction $ g $ définie sur $ \mathbb{R} $ par $ g(x) = x^2 \ln \left(x^2 + 4\right) $.
Alors $ \displaystyle\int_0^2 g'(x)\:\text{d}x $ vaut, à $ 10^{-1} $ près :- 4,9
- 8,3
- 1,7
- 7,5
- Une professeure enseigne la spécialité mathématiques dans une classe de 31 élèves de terminale.
Elle veut former un groupe de 5 élèves. De combien de façons différentes peut-elle former un tel groupe de 5 élèves ?- $ 31^5 $
- $ 31\times30\times29\times28\times27 $
- $ 31+30+29+28+27 $
- $ \dbinom{31}{5} $
- La professeure s'intéresse maintenant à l'autre spécialité des 31 élèves de son groupe :
- 10 élèves ont choisi la spécialité physique-chimie ;
- 20 élèves ont choisi la spécialité SES ;
- 1 élève a choisi la spécialité LLCE espagnol.
Elle veut former un groupe de 5 élèves comportant exactement 3 élèves ayant choisi la spécialité SES. De combien de façons différentes peut-elle former un tel groupe ?
- $ \displaystyle\binom{20}{3} \times \binom{11}{2} $
- $ \displaystyle\binom{20}{3} + \binom{11}{2} $
- $ \displaystyle\binom{20}{3} $
- $ 20^3 \times 11^2 $
Contenu Premium
Cette vidéo explicative fait partie de notre contenu premium. Abonnez-vous pour accéder à toutes les méthodes détaillées.
Avec l'abonnement premium :
- Vidéos explicatives détaillées
- Accès à toutes les méthodes
- Exercices corrigés inclus
- Support prioritaire