Sujets de Bac
2024
Dérivation et convexité
Filtrer par chapitre
Amerique Du Nord 21 Mai 2024 Jour 1
1 exercice
Le but de cet exercice est d’étudier la fonction $ f $ définie sur l’intervalle $ ]0 ; +\infty[ $ par: $$f(x) = x\ln(x^2) - \frac{1}{x}$$
Partie A : lectures graphiques
On a tracé ci-dessous la courbe représentative $(\mathcal{C}_f)$ de la fonction $ f $, ainsi que la droite $(T)$, tangente à la courbe $(\mathcal{C}_f)$ au point $A(1;~-1)$.
Cette tangente passe également par le point $B(0;~-4)$.
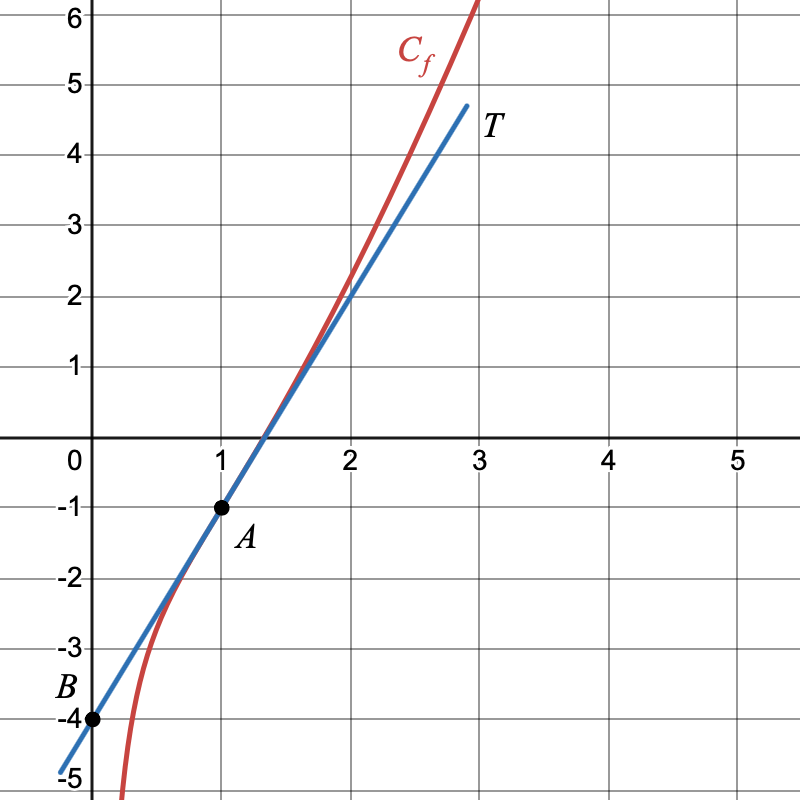
- Lire graphiquement $f'(1)$ et donner l’équation réduite de la tangente $(T)$.
- Donner les intervalles sur lesquels la fonction $ f $ semble convexe ou concave. Que semble représenter le point A pour la courbe $(\mathcal{C}_f)$ ?
Partie B : étude analytique
- Déterminer, en justifiant, la limite de $ f $ en $+\infty$, puis sa limite en 0.
- On admet que la fonction $ f $ est deux fois dérivable sur l’intervalle $ ]0 ; +\infty[ $.
- Déterminer $ f'(x) $ pour $ x $ appartenant à l’intervalle $ ]0 ; +\infty[ $.
- Montrer que pour tout $ x $ appartenant à l’intervalle $ ]0 ; +\infty[ $, $$f''(x) = \frac{2(x+1)(x-1)}{x^3}$$
-
- Étudier la convexité de la fonction $ f $ sur l’intervalle $ ]0 ; +\infty[ $.
- Étudier les variations de la fonction $ f' $, puis le signe de $ f'(x) $ pour $ x $ appartenant à l’intervalle $ ]0 ; +\infty[ $.
En déduire le sens de variation de la fonction $ f $ sur l’intervalle $ ]0 ; +\infty[ $.
-
- Montrer que l’équation $ f(x) = 0 $ admet une unique solution $ \alpha $ sur l’intervalle $ ]0 ; +\infty[ $.
- Donner la valeur arrondie au centième de $ \alpha $ et montrer que $ \alpha $ vérifie : $$\alpha^2 = \exp\left( \frac{1}{\alpha^2} \right)$$
Asie 10 Juin 2024 Jour 1
1 exercice
Partie A
On considère une fonction $ f $ définie sur $ [0 ; +\infty[ $, représentée par la courbe $C_f$ ci-dessous.
La droite $ T $ est tangente à la courbe $C_f$ au point $ A $ d'abscisse $\dfrac{5}{2}$.
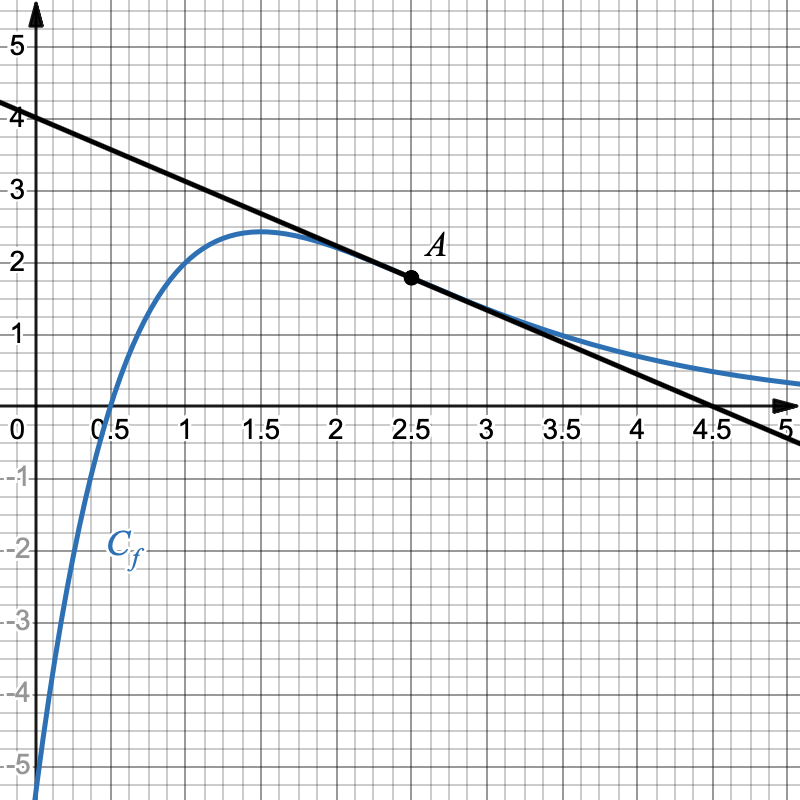
- Dresser, par lecture graphique, le tableau des variations de la fonction $ f $ sur l’intervalle $ [0 ; 5] $.
- Que semble présenter la courbe $C_f$ au point $ A $ ?
- La dérivée $ f' $ et la dérivée seconde $ f'' $ de la fonction $ f $ sont représentées par les courbes ci-dessous.
Associer à chacune de ces deux fonctions la courbe qui la représente.
Ce choix sera justifié. 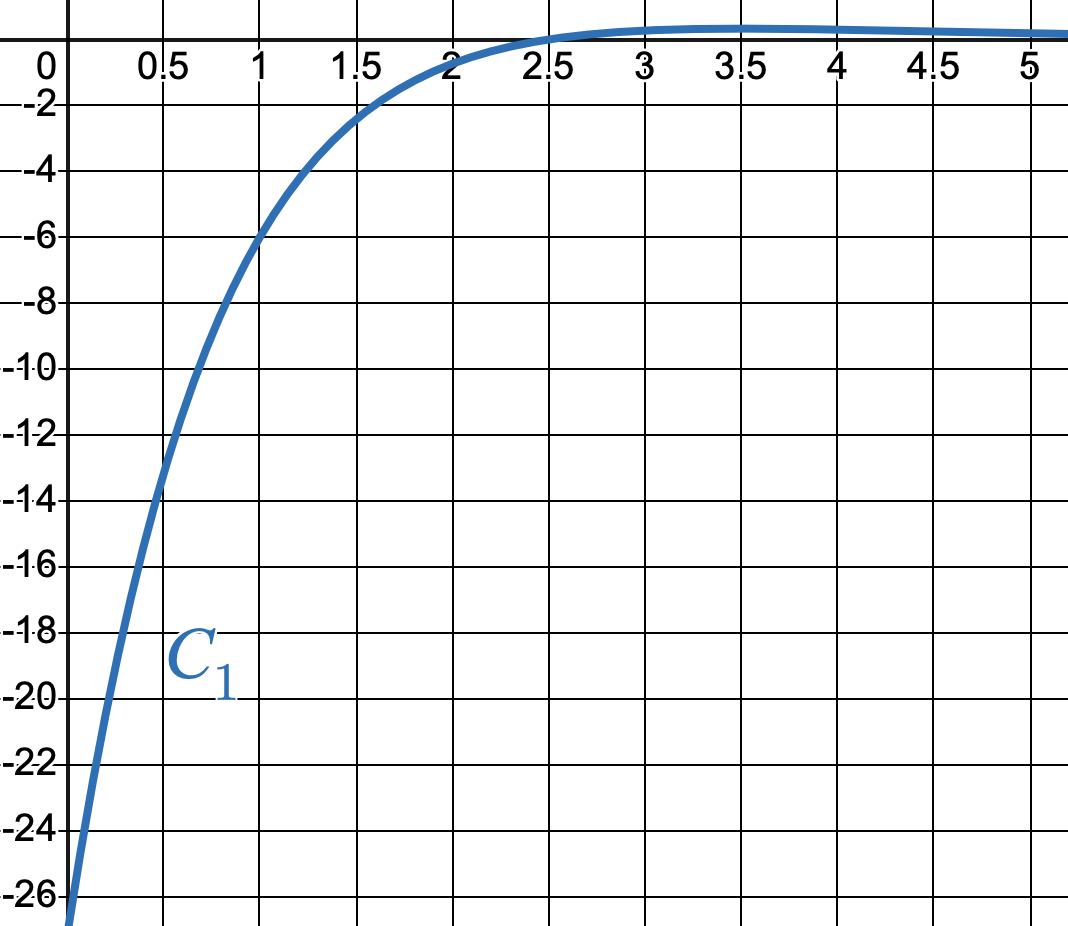
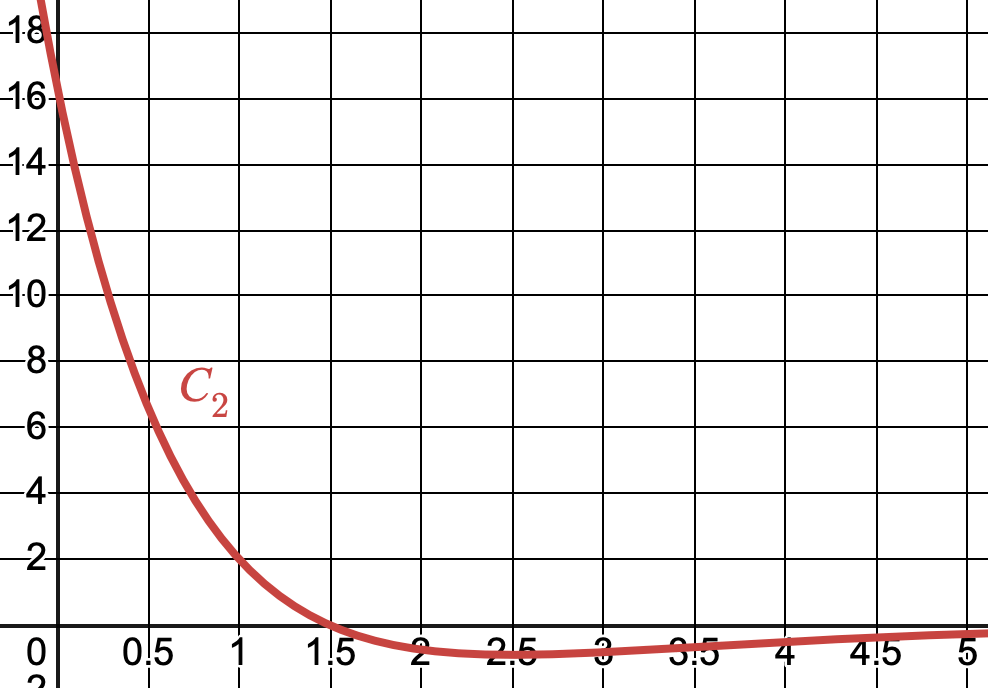
-
-
La courbe $C_3 $ ci-contre peut-elle être la représentation graphique sur $ [0 ; +\infty[ $ d’une primitive de la fonction $f$ ? Justifier.
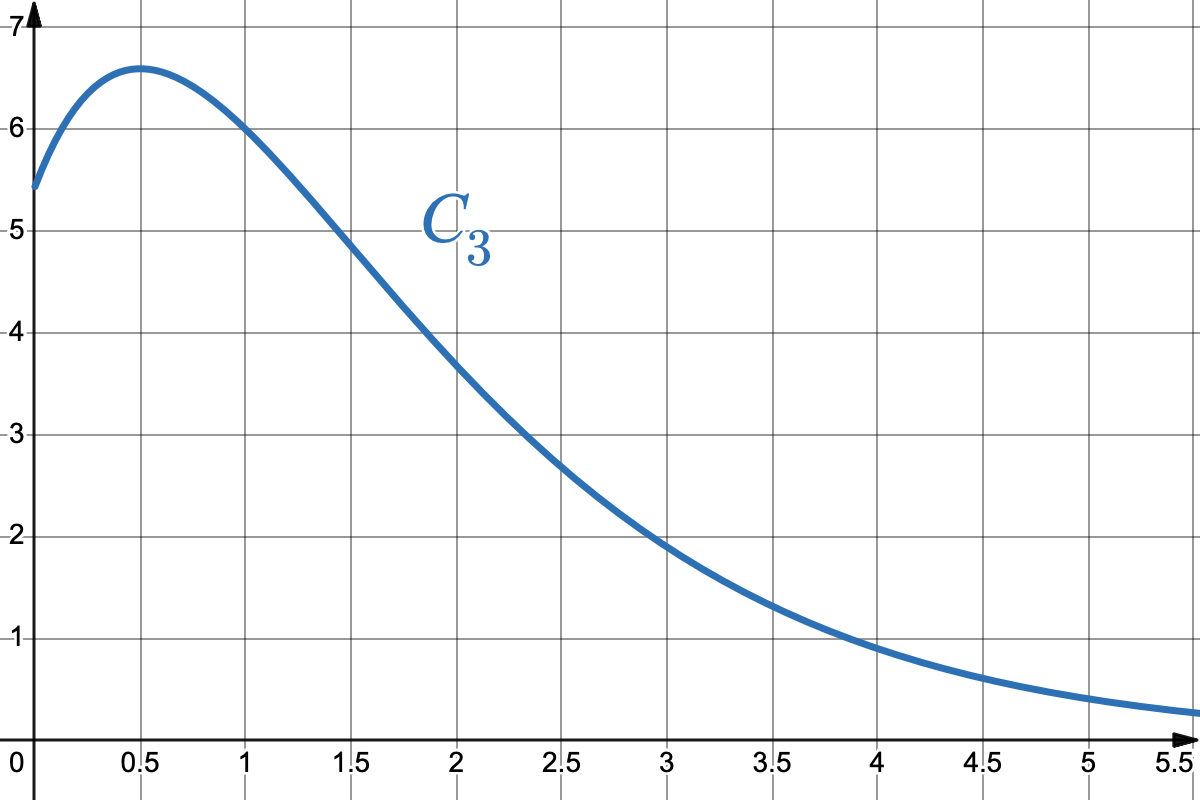
-
Partie B
Dans cette partie, on considère que la fonction $ f $, définie et deux fois dérivable sur $ [0 ; +\infty[ $, est définie par : $$ f(x) = (4x - 2)e^{-x+1}. $$
On notera respectivement $ f' $ et $ f'' $ la dérivée et la dérivée seconde de la fonction $ f $.
- Étude de la fonction $ f $
- Montrer que $ f'(x) = (-4x + 6)e^{-x+1} $.
- Utiliser ce résultat pour déterminer le tableau complet des variations de la fonction $ f $ sur $ [0 ; +\infty[ $. On admet que $\lim\limits_{x \to +\infty} f(x) = 0 $.
- Étudier la convexité de la fonction $ f $ et préciser l'abscisse d'un éventuel point d'inflexion de la courbe représentative de $ f $.
- On considère une fonction $ F $ définie sur $ [0 ; +\infty[ $ par $ F(x) = (ax + b)e^{-x+1} $, où $ a $ et $ b $ sont deux nombres réels.
- Déterminer les valeurs des réels $ a $ et $ b $ telles que la fonction $ F $ soit une primitive de la fonction $ f $ sur $ [0 ; +\infty[ $.
- On admet que $ F(x) = (-4x - 2)e^{-x+1} $ est une primitive de la fonction $ f $ sur $ [0 ; +\infty[ $.
En déduire la valeur exacte, puis une valeur approchée à $ 10^{-2} $ près, de l'intégrale $$ I = \int_{\frac{3}{2}}^{8} f(x) \, dx. $$
-
-
Une municipalité a décidé de construire une piste de trottinette freestyle.
Le profil de cette piste est donné par la courbe représentative de la fonction $ f $ sur l'intervalle $ [\dfrac{3}{2} ; 8] $.
L'unité de longueur est le mètre. 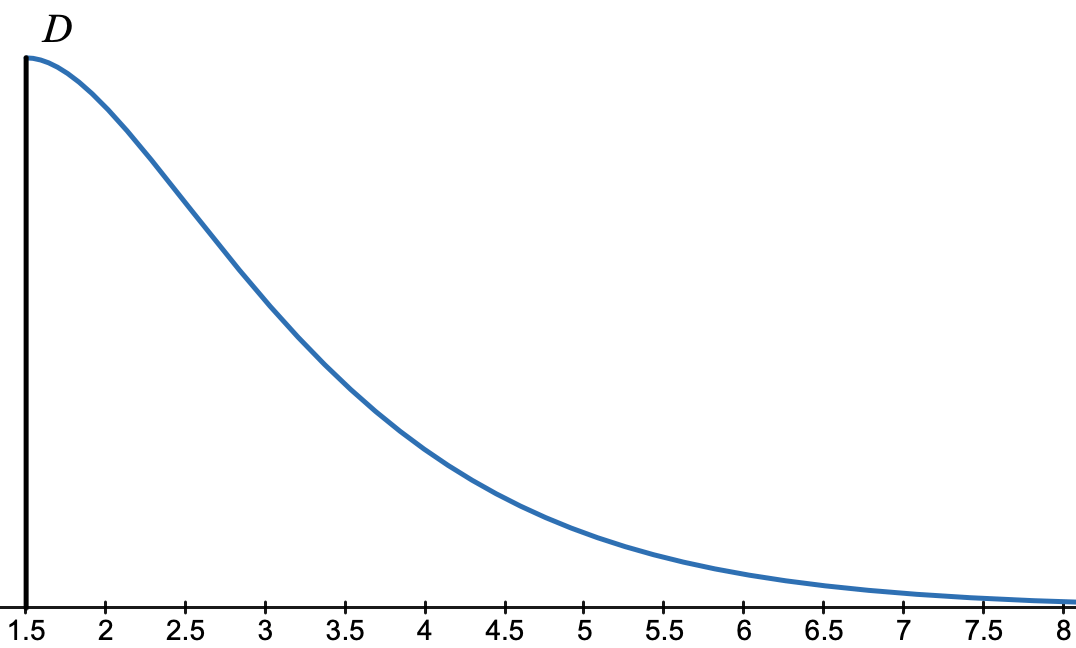
- Donner une valeur approchée au cm près de la hauteur du point de départ $ D $.
- La municipalité a organisé un concours de graffiti pour orner le mur de profil de la piste. L'artiste retenue prévoit de couvrir environ 75 % de la surface du mur.
Sachant qu'une bombe aérosol de 150 mL permet de couvrir une surface de 0,8 m$ ^2 $, déterminer le nombre de bombes qu'elle devra utiliser pour réaliser cette œuvre.
-
Asie 11 Juin 2024 Jour 2
1 exercice
Pour chacune des affirmations suivantes, indiquer si elle est vraie ou fausse. Chaque réponse doit être justifiée. Une réponse non justifiée ne rapporte aucun point.
-
Soit $ (u_n) $ une suite définie pour tout entier naturel $ n $ et vérifiant la relation suivante :
$$ \dfrac{1}{2} < u_n \leq \dfrac{3n^2 + 4n + 7}{6n^2 + 1} \text{ pour tout entier naturel } n $$.
Affirmation 1 : $ \lim\limits_{n \to +\infty} u_n = \dfrac{1}{2} $.
-
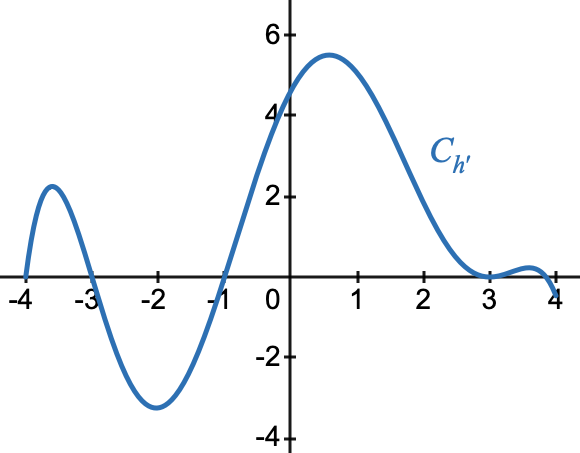
Soit $ h $ une fonction définie et dérivable sur l’intervalle $[-4 ; 4]$. La représentation graphique $ \mathcal{C}_{h'} $ de sa fonction dérivée $ h' $ est donnée ci-dessous.
Affirmation 2 : La fonction $ h $ est convexe sur $[-1 ; 3]$.
-
Le code d’un immeuble est composé de 4 chiffres (qui peuvent être identiques) suivis de deux lettres distinctes parmi A, B et C (exemple : 1232BA).
Affirmation 3 : Il existe 20 634 codes qui contiennent au moins un 0.
-
On considère la fonction $ f $ définie sur $ \left] 0 ; +\infty \right[ $ par $ f(x) = x \ln x $.
Affirmation 4 : La fonction $ f $ est une solution sur $ \left] 0 ; +\infty \right[ $ de l’équation différentielle
$$ x y' - y = x $$.
Centres Etrangers 6 Juin 2024 Jour 2
1 exercice
On considère la fonction $ f $ définie sur l’intervalle $ ]-\infty ; 1[ $ par : $$ f(x) = \frac{e^x}{x - 1}. $$
On admet que la fonction $ f $ est dérivable sur l’intervalle $ ]-\infty ; 1[ $.
On appelle $ \mathcal{C} $ sa courbe représentative dans un repère.
-
- Déterminer la limite de la fonction $ f $ en 1.
- En déduire une interprétation graphique.
- Déterminer la limite de la fonction $ f $ en $ -\infty $.
-
- Montrer que pour tout réel $ x $ de l’intervalle $ ]-\infty ; 1[ $, on a : $$ f'(x) = \frac{(x - 2)e^x}{(x - 1)^2}. $$
- Dresser, en justifiant, le tableau de variations de la fonction $ f $ sur l’intervalle $ ]-\infty ; 1[ $.
- On admet que pour tout réel $ x $ de l’intervalle $ ] - \infty ; 1[ $, on a :
$$
f''(x) = \frac{(x^2 - 4x + 5)e^x}{(x - 1)^3}.
$$
- Étudier la convexité de la fonction $ f $ sur l’intervalle $ ]-\infty ; 1[ $.
- Déterminer l’équation réduite de la tangente $ T $ à la courbe $ \mathcal{C} $ au point d’abscisse 0.
- En déduire que, pour tout réel $ x $ de l’intervalle $ ]-\infty ; 1[ $, on a : $$ e^x \geq (-2x - 1)(x - 1). $$
-
- Justifier que l’équation $ f(x) = -2 $ admet une unique solution $ \alpha $ sur l’intervalle $ ]-\infty ; 1[ $.
- À l’aide de la calculatrice, déterminer un encadrement de $ \alpha $ d’amplitude $ 10^{-2} $.
Metropole 19 Juin 2024 Jour 1
1 exercice
Partie A : étude de la fonction $f$
La fonction $f$ est définie sur l'intervalle $]0 ~;~+\infty[$ par :
$f(x) = x - 2 + \dfrac{1}{2} \ln x,$
où $\ln$ désigne la fonction logarithme népérien. On admet que la fonction $f$ est deux fois dérivable sur $]0 ~;~ +\infty[$. On note $f'$ sa dérivée et $f''$ sa dérivée seconde.
-
- Déterminer, en justifiant, les limites de $f$ en 0 et en $+\infty$.
- Montrer que pour tout $x$ appartenant à $]0 ~;~+\infty[$, on a : $f'(x) = \dfrac{2x + 1}{2x}$.
- Étudier le sens de variation de $f$ sur $]0 ~;~+\infty[$.
- Étudier la convexité de $f$ sur $]0 ~;~+\infty[$.
-
- Montrer que l'équation $f(x) = 0$ admet dans $]0 ~;~+\infty[$ une solution unique qu'on notera $\alpha$ et justifier que $\alpha$ appartient à l'intervalle $[1~;~2]$.
- Déterminer le signe de $f(x)$ pour $x \in ]0 ~;~+\infty[$.
- Montrer que $\ln(\alpha) = 2(2-\alpha)$.
Partie B : étude de la fonction $g$
La fonction $g$ est définie sur $]0~;~1]$ par :
$g(x) = -\dfrac{7}{8}x^{2} + x - \dfrac{1}{4}x^{2}\ln x.$
On admet que la fonction $g$ est dérivable sur $]0~;~1]$ et on note $g'$ sa fonction dérivée.
- Calculer $g'(x)$ pour $x \in ]0~;~1]$ puis vérifier que $g'(x) = x f\left(\dfrac{1}{x}\right)$.
-
- Justifier que pour $x$ appartenant à l'intervalle $\left]0~;~\dfrac{1}{\alpha}\right[$, on a $f\left(\dfrac{1}{x}\right) > 0$.
- On admet le tableau de signes suivant :
En déduire le tableau de variations de $g$ sur l'intervalle $]0~;~1]$. Les images et les limites ne sont pas demandées.

Partie C : un calcul d'aire
On a représenté sur le graphique ci-dessous :
- La courbe $\mathcal{C}_{g}$ de la fonction $g$ ;
- La parabole $\mathcal{P}$ d'équation $y = -\dfrac{7}{8}x^{2} + x$ sur l'intervalle $]0~;~1]$.
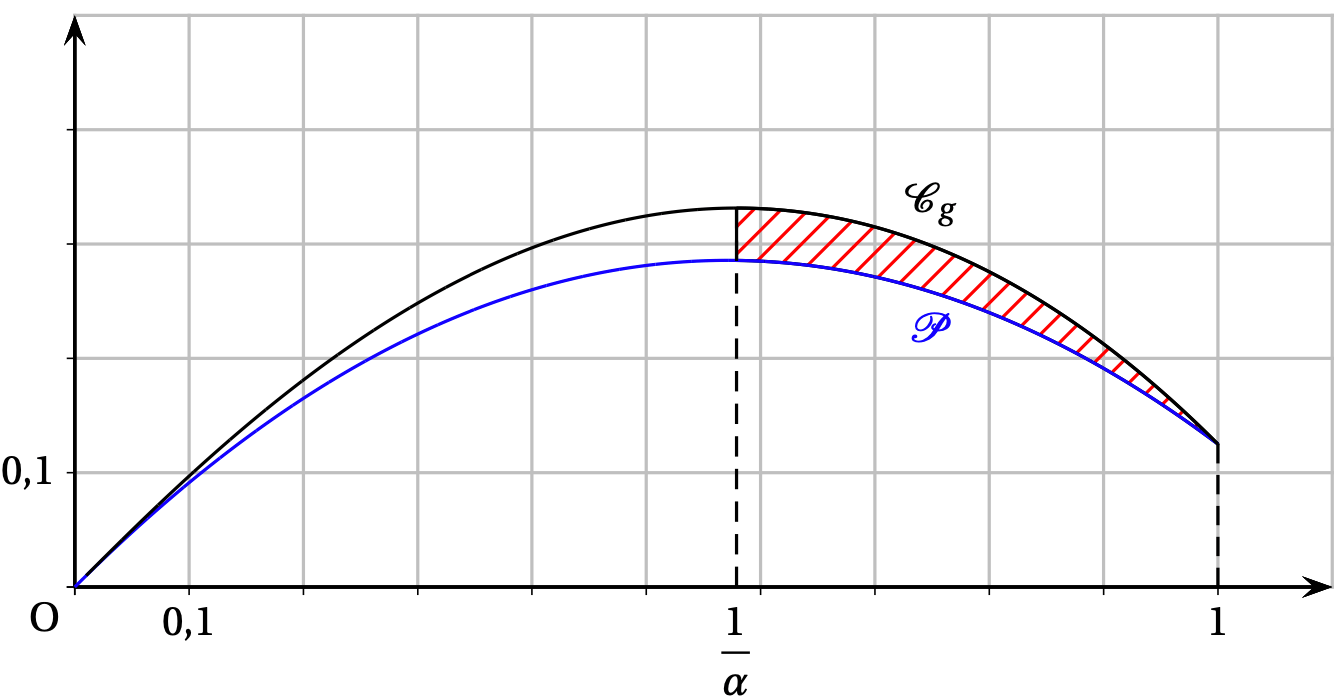
On souhaite calculer l'aire $\mathcal{A}$ du domaine hachuré compris entre les courbes $\mathcal{C}_{g}$ et $\mathcal{P}$, et les droites d'équations $x = \dfrac{1}{\alpha}$ et $x = 1$.
On rappelle que $\ln(\alpha) = 2(2-\alpha)$.
-
- Justifier la position relative des courbes $\mathcal{C}_{g}$ et $\mathcal{P}$ sur l'intervalle $\left]0~;~1\right]$.
- Démontrer l'égalité :
$$ \int_{\frac{1}{\alpha}}^{1} x^{2} \ln x \,\mathrm{d}x = \dfrac{-\alpha^{3} - 6\alpha + 13}{9\alpha^{3}}. $$
- En déduire l'expression en fonction de $\alpha$ de l'aire $\mathcal{A}$.
Metropole 20 Juin 2024 Jour 2
1 exercice
On considère une fonction $f$ définie et deux fois dérivable sur $]-2 ~;~+\infty[$. On note $ \mathcal{C}_{f} $ sa courbe représentative dans un repère orthogonal du plan, $f'$ sa dérivée et $f''$ sa dérivée seconde.
On a tracé ci-dessous la courbe $ \mathcal{C}_{f} $ et sa tangente $T$ au point $B$ d'abscisse $-1$.
On précise que la droite $T$ passe par le point $A(0 ~;~ -1)$.
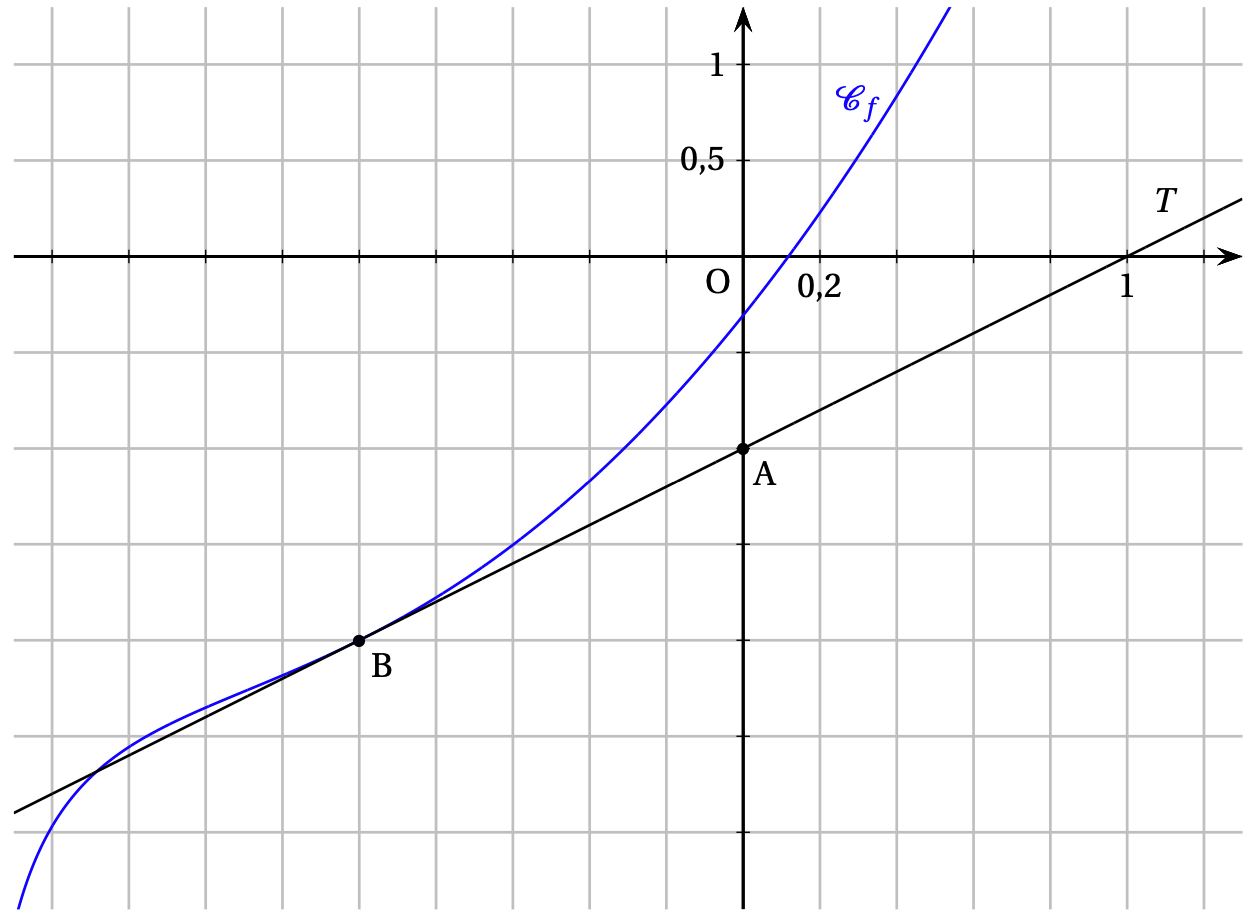
Partie A : exploitation du graphique.
À l'aide du graphique, répondre aux questions ci-dessous.
- Préciser $f(-1)$ et $f'(-1)$.
- La fonction $f$ est-elle convexe sur son ensemble de définition ? Justifier.
- Conjecturer le nombre de solutions de l'équation $f(x) = 0$ et donner une valeur arrondie à $10^{-1}$ près d'une solution.
Partie B : étude de la fonction $f$
On considère que la fonction $f$ est définie sur $]-2 ~;~+\infty[$ par :
$$ f(x) = x^{2}+ 2x - 1 + \ln (x + 2), $$
où $\ln$ désigne la fonction logarithme népérien.
- Déterminer par le calcul la limite de la fonction $f$ en $-2$. Interpréter graphiquement ce résultat.
On admet que $\lim\limits_{x \to +\infty} f(x)=+\infty$. - Montrer que pour tout $x>-2, \quad f'(x)=\dfrac{2 x^{2}+6 x+5}{x+2}$.
- Étudier les variations de la fonction $f$ sur $]-2 ~;~+\infty[$ puis dresser son tableau de variations complet.
- Montrer que l'équation $f(x)=0$ admet une unique solution $\alpha$ sur $]-2 ~;~+\infty[$ et donner une valeur arrondie de $\alpha$ à $10^{-2}$ près.
- En déduire le signe de $f(x)$ sur $]-2~;~ +\infty[$.
- Montrer que $\mathcal{C}_{f}$ admet un unique point d'inflexion et déterminer son abscisse.
Partie C : une distance minimale.
Soit $g$ la fonction définie sur $]-2 ~;~ +\infty[$ par $~g(x)=\ln (x+2)$.
On note $\mathcal{C}_{g}$ sa courbe représentative dans un repère orthonormé $(\mathrm{0} ~;~ \mathrm{I}~,~ \mathrm{J})$.
Soit $M$ un point de $\mathcal{C}_{g}$ d'abscisse $x$.
Le but de cette partie est de déterminer pour quelle valeur de $x$ la distance $\mathrm{J}M$ est minimale.
On considère la fonction $h$ définie sur $]-2 ~;~ +\infty[$ par $~h(x)=\mathrm{J}M^{2}$.
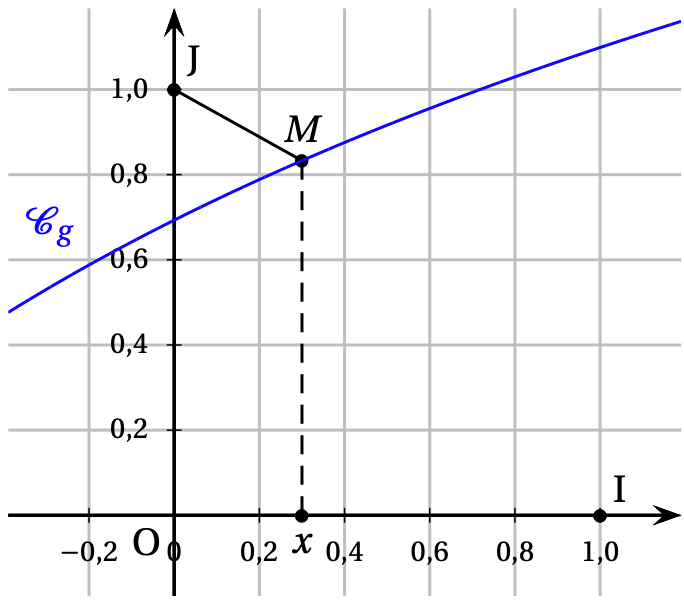
- Justifier que pour tout $x>-2$, on a :$~~h(x)=x^{2}+[\ln (x+2)-1]^{2}.$
-
- On admet que la fonction $h$ est dérivable sur $]-2 ~;~ +\infty[$ et on note $h'$ sa fonction dérivée.
- On admet également que pour tout réel $x>-2$, $$ h'(x)=\dfrac{2 f(x)}{x+2} $$ où $f$ est la fonction étudiée en partie B.
- Dresser le tableau de variations de $h$ sur $]-2 ~;~ +\infty[$.
Les limites ne sont pas demandées. - En déduire que la valeur de $x$ pour laquelle la distance $\mathrm{J}M$ est minimale est $\alpha$ où $\alpha$ est le nombre réel défini à la question 4. de la partie B.
-
- On notera $M_{\alpha}$ le point de $\mathcal{C}_{g}$ d'abscisse $\alpha$.
- Montrer que $~\ln (\alpha+2)=1-2 \alpha-\alpha^{2}.$
- En déduire que la tangente à $\mathcal{C}_{g}$ au point $M_{\alpha}$ et la droite $(\mathrm{J}M_{\alpha})$ sont perpendiculaires.
- On pourra utiliser le fait que, dans un repère orthonormé, deux droites sont perpendiculaires lorsque le produit de leurs coefficients directeurs est égal à $-1$.
Contenu Premium
Cette vidéo explicative fait partie de notre contenu premium. Abonnez-vous pour accéder à toutes les méthodes détaillées.
Avec l'abonnement premium :
- Vidéos explicatives détaillées
- Accès à toutes les méthodes
- Exercices corrigés inclus
- Support prioritaire