Sujets de Bac
2024
Calcul intégral
Filtrer par chapitre
Amerique Du Nord 21 Mai 2024 Jour 1
1 exercice
Pour tout entier naturel $ n $, on considère les intégrales suivantes : $$I_n = \int_{0}^{\pi} e^{-nx}\sin(x)\,dx, \quad J_n = \int_{0}^{\pi} e^{-nx}\cos(x)\,dx.$$
- Calculer $ I_0 $.
-
- Justifier que, pour tout entier naturel $ n $, on a $ I_n \geq 0 $.
- Montrer que, pour tout entier naturel $ n $, on a $ I_{n+1} - I_n \leq 0 $.
- Déduire des deux questions précédentes que la suite $ (I_n) $ converge.
-
- Montrer que, pour tout entier naturel $ n $, on a : $$ I_n \leq \int_{0}^{\pi} e^{-nx}\,dx. $$
- Montrer que, pour tout entier naturel $ n \geq 1 $, on a : $$ \int_{0}^{\pi} e^{-nx}\,dx = \frac{1 - e^{-n\pi}}{n}. $$
- Déduire des deux questions précédentes la limite de la suite $ (I_n) $.
-
- En intégrant par parties l’intégrale $ I_n $ de deux façons différentes, établir les deux relations suivantes, pour tout entier naturel $ n \geq 1 $ : $$ I_n = 1 + e^{-n\pi} - nJ_n \quad \text{et} \quad I_n = \frac{1}{n}J_n. $$
- En déduire que, pour tout entier naturel $ n \geq 1 $, on a : $$ I_n = \frac{1 + e^{-n\pi}}{n^2 + 1}. $$
- On souhaite obtenir le rang $ n $ à partir duquel la suite $ (I_n) $ devient inférieure à 0,1.
Recopier et compléter la cinquième ligne du script Python ci-dessous avec la commande appropriée.

Amerique Du Nord 22 Mai 2024 Jour 2
1 exercice
Soit $ a $ un réel strictement positif.
On considère la fonction $ f $ définie sur l’intervalle $ ]0 ; +\infty[ $ par :
$$f(x) = a\ln(x).$$
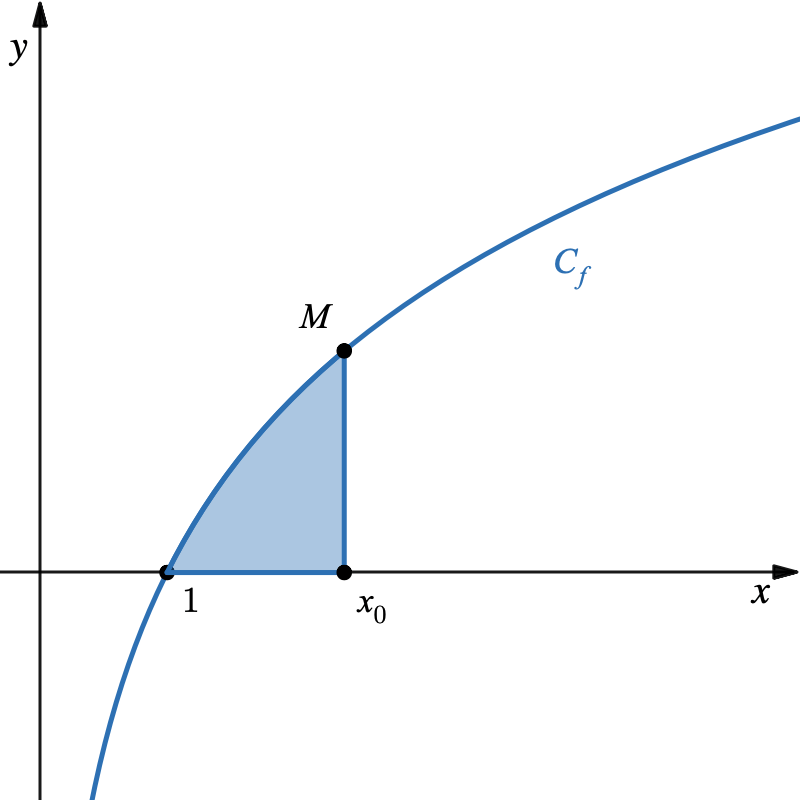
On note $C_f$ sa courbe représentative dans un repère orthonormé.
Soit $ x_0 $ un réel strictement supérieur à 1.
- Déterminer l’abscisse du point d’intersection de la courbe $C_f$ et de l’axe des abscisses.
- Vérifier que la fonction $ F $ définie par $ F(x) = a[x\ln(x) - x] $ est une primitive de la fonction $ f $ sur l’intervalle $ ]0 ; +\infty[ $.
- En déduire l’aire du domaine bleuté en fonction de $ a $ et de $ x_0 $.
- Démontrer que la longueur $ AB $ est égale à une constante (c’est-à-dire à un nombre qui ne dépend pas de $ x_0 $) que l’on déterminera.
Le candidat prendra soin d’expliciter sa démarche.
On note $ T $ la tangente à la courbe $C_f$ au point $ M $ d’abscisse $ x_0 $.
On appelle $ A $ le point d’intersection de la tangente $ T $ avec l’axe des ordonnées et $ B $ le projeté orthogonal de $ M $ sur l’axe des ordonnées.
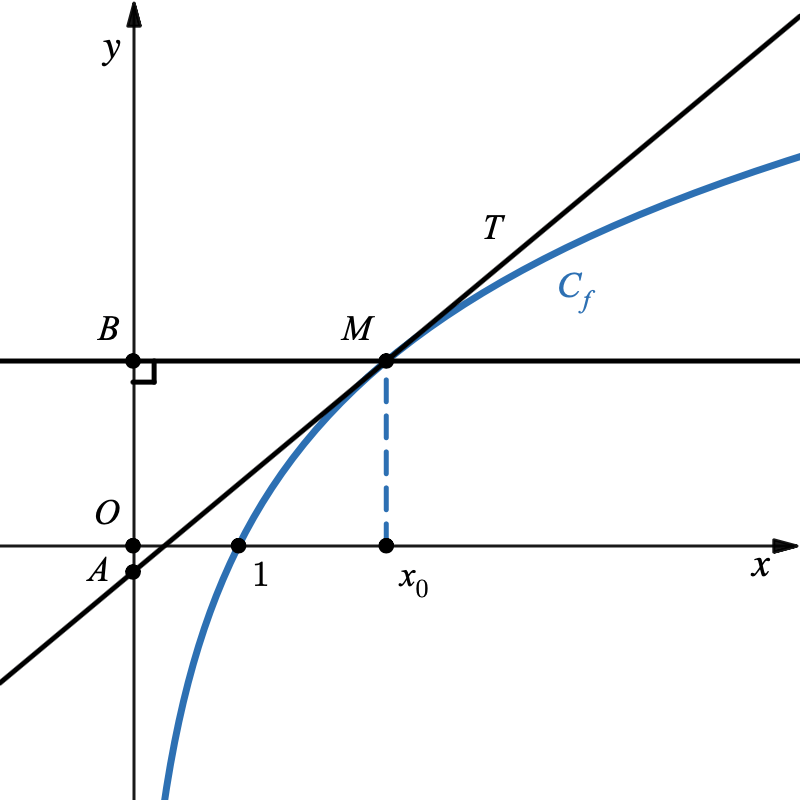
Asie 10 Juin 2024 Jour 1
1 exercice
Partie A
On considère une fonction $ f $ définie sur $ [0 ; +\infty[ $, représentée par la courbe $C_f$ ci-dessous.
La droite $ T $ est tangente à la courbe $C_f$ au point $ A $ d'abscisse $\dfrac{5}{2}$.
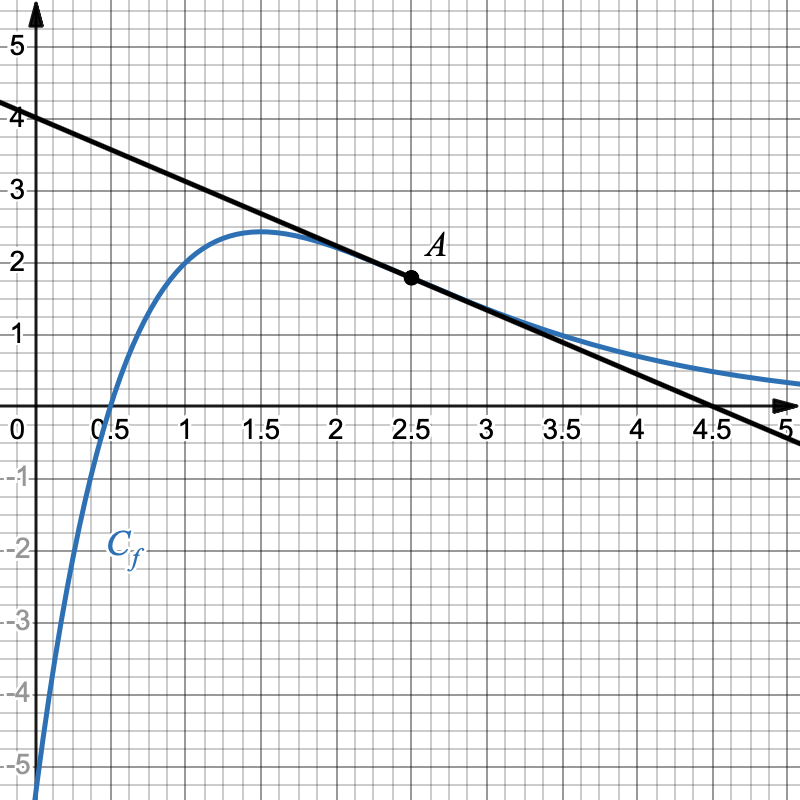
- Dresser, par lecture graphique, le tableau des variations de la fonction $ f $ sur l’intervalle $ [0 ; 5] $.
- Que semble présenter la courbe $C_f$ au point $ A $ ?
- La dérivée $ f' $ et la dérivée seconde $ f'' $ de la fonction $ f $ sont représentées par les courbes ci-dessous.
Associer à chacune de ces deux fonctions la courbe qui la représente.
Ce choix sera justifié. 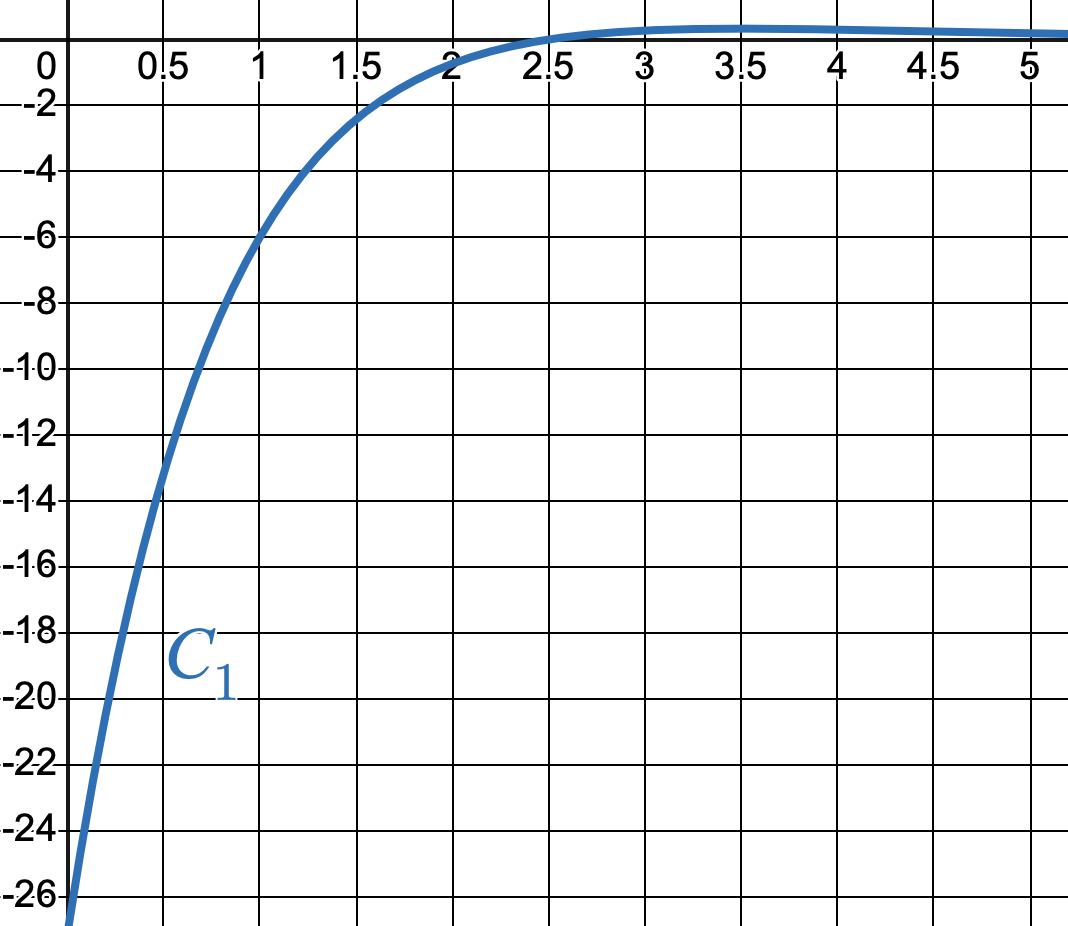
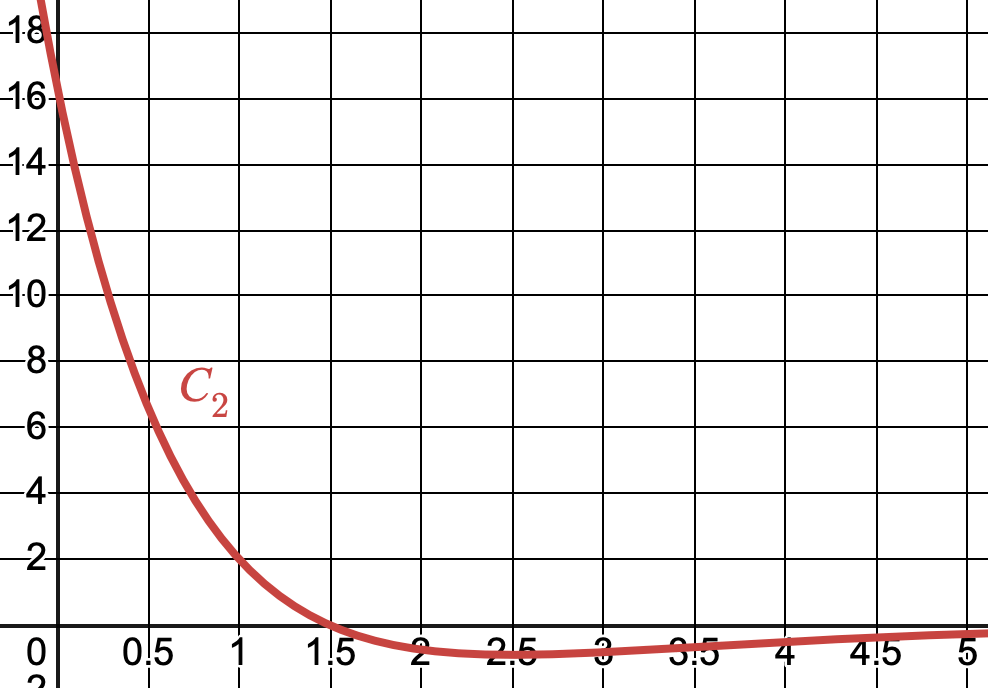
-
-
La courbe $C_3 $ ci-contre peut-elle être la représentation graphique sur $ [0 ; +\infty[ $ d’une primitive de la fonction $f$ ? Justifier.
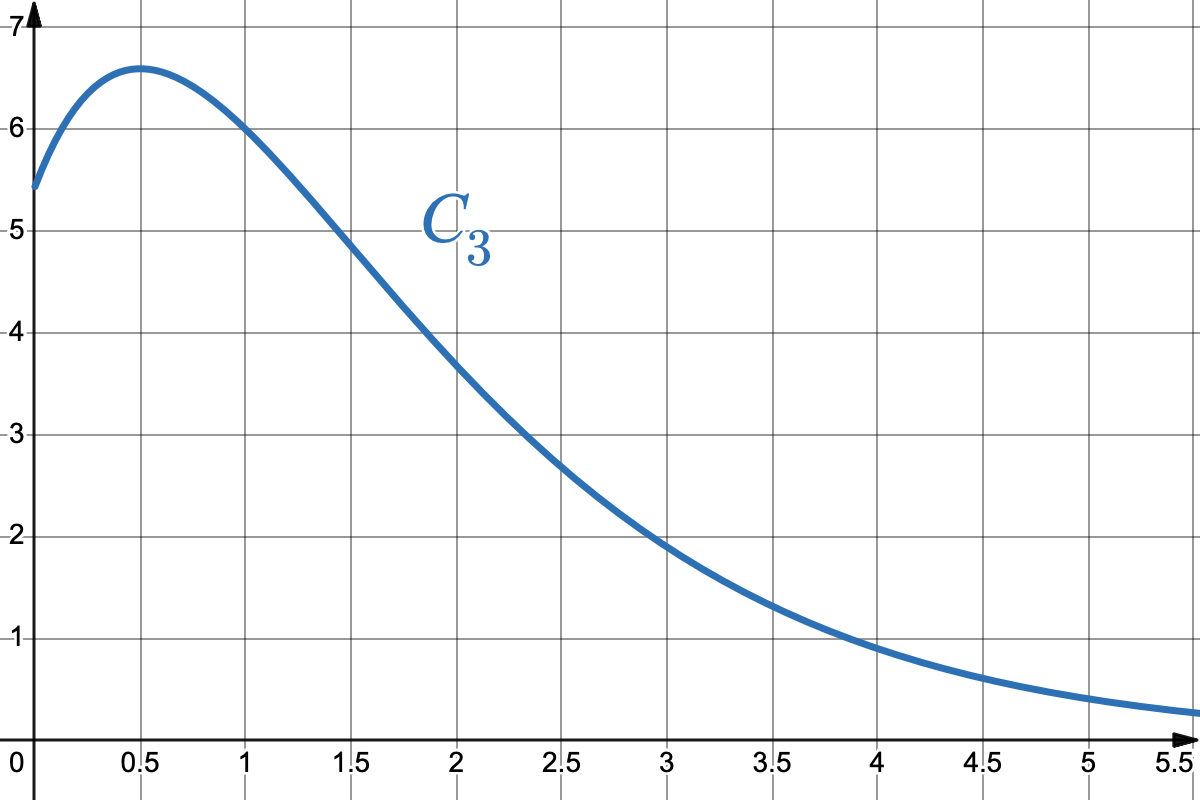
-
Partie B
Dans cette partie, on considère que la fonction $ f $, définie et deux fois dérivable sur $ [0 ; +\infty[ $, est définie par : $$ f(x) = (4x - 2)e^{-x+1}. $$
On notera respectivement $ f' $ et $ f'' $ la dérivée et la dérivée seconde de la fonction $ f $.
- Étude de la fonction $ f $
- Montrer que $ f'(x) = (-4x + 6)e^{-x+1} $.
- Utiliser ce résultat pour déterminer le tableau complet des variations de la fonction $ f $ sur $ [0 ; +\infty[ $. On admet que $\lim\limits_{x \to +\infty} f(x) = 0 $.
- Étudier la convexité de la fonction $ f $ et préciser l'abscisse d'un éventuel point d'inflexion de la courbe représentative de $ f $.
- On considère une fonction $ F $ définie sur $ [0 ; +\infty[ $ par $ F(x) = (ax + b)e^{-x+1} $, où $ a $ et $ b $ sont deux nombres réels.
- Déterminer les valeurs des réels $ a $ et $ b $ telles que la fonction $ F $ soit une primitive de la fonction $ f $ sur $ [0 ; +\infty[ $.
- On admet que $ F(x) = (-4x - 2)e^{-x+1} $ est une primitive de la fonction $ f $ sur $ [0 ; +\infty[ $.
En déduire la valeur exacte, puis une valeur approchée à $ 10^{-2} $ près, de l'intégrale $$ I = \int_{\frac{3}{2}}^{8} f(x) \, dx. $$
-
-
Une municipalité a décidé de construire une piste de trottinette freestyle.
Le profil de cette piste est donné par la courbe représentative de la fonction $ f $ sur l'intervalle $ [\dfrac{3}{2} ; 8] $.
L'unité de longueur est le mètre. 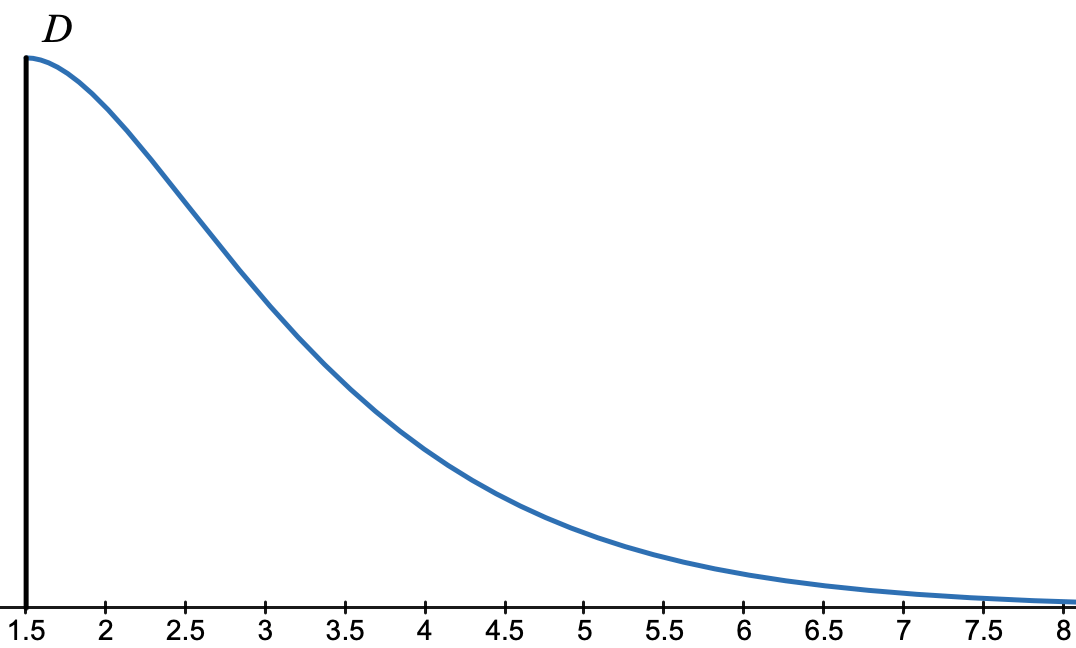
- Donner une valeur approchée au cm près de la hauteur du point de départ $ D $.
- La municipalité a organisé un concours de graffiti pour orner le mur de profil de la piste. L'artiste retenue prévoit de couvrir environ 75 % de la surface du mur.
Sachant qu'une bombe aérosol de 150 mL permet de couvrir une surface de 0,8 m$ ^2 $, déterminer le nombre de bombes qu'elle devra utiliser pour réaliser cette œuvre.
-
Centres Etrangers 5 Juin 2024 Jour 1
1 exercice
On considère l’équation différentielle $$(E_0) : y' = y $$ où $ y $ est une fonction dérivable de la variable réelle $ x $.
- Démontrer que l’unique fonction constante solution de l’équation différentielle $ (E_0) $ est la fonction nulle.
- Déterminer toutes les solutions de l’équation différentielle $ (E_0) $.
- La fonction $ h $ est définie sur $ \mathbb{R} $ par $ h(x) = 2 \cos(x) + \sin(x) $.
On admet qu’elle est dérivable sur $ \mathbb{R} $.
Démontrer que la fonction $ h $ est solution de l’équation différentielle $ (E) $. - On considère une fonction $ f $ définie et dérivable sur $ \mathbb{R} $.
Démontrer que : « $ f $ est solution de $ (E) $ » est équivalent à « $ f - h $ est solution de $(E_0)$ ». - En déduire toutes les solutions de l’équation différentielle $ (E) $.
- Déterminer l’unique solution $ g $ de l’équation différentielle $ (E) $ telle que $ g(0) = 0 $.
- Calculer : $$ \int_{0}^{\frac{\pi}{2}} \left[-2e^x + \sin(x) + 2 \cos(x)\right] \mathrm{d}x. $$
On considère l’équation différentielle $$ (E) : y' = y - \cos(x) - 3 \sin(x) $$ où $ y $ est une fonction dérivable de la variable réelle $ x $.
Metropole 19 Juin 2024 Jour 1
1 exercice
Partie A : étude de la fonction $f$
La fonction $f$ est définie sur l'intervalle $]0 ~;~+\infty[$ par :
$f(x) = x - 2 + \dfrac{1}{2} \ln x,$
où $\ln$ désigne la fonction logarithme népérien. On admet que la fonction $f$ est deux fois dérivable sur $]0 ~;~ +\infty[$. On note $f'$ sa dérivée et $f''$ sa dérivée seconde.
-
- Déterminer, en justifiant, les limites de $f$ en 0 et en $+\infty$.
- Montrer que pour tout $x$ appartenant à $]0 ~;~+\infty[$, on a : $f'(x) = \dfrac{2x + 1}{2x}$.
- Étudier le sens de variation de $f$ sur $]0 ~;~+\infty[$.
- Étudier la convexité de $f$ sur $]0 ~;~+\infty[$.
-
- Montrer que l'équation $f(x) = 0$ admet dans $]0 ~;~+\infty[$ une solution unique qu'on notera $\alpha$ et justifier que $\alpha$ appartient à l'intervalle $[1~;~2]$.
- Déterminer le signe de $f(x)$ pour $x \in ]0 ~;~+\infty[$.
- Montrer que $\ln(\alpha) = 2(2-\alpha)$.
Partie B : étude de la fonction $g$
La fonction $g$ est définie sur $]0~;~1]$ par :
$g(x) = -\dfrac{7}{8}x^{2} + x - \dfrac{1}{4}x^{2}\ln x.$
On admet que la fonction $g$ est dérivable sur $]0~;~1]$ et on note $g'$ sa fonction dérivée.
- Calculer $g'(x)$ pour $x \in ]0~;~1]$ puis vérifier que $g'(x) = x f\left(\dfrac{1}{x}\right)$.
-
- Justifier que pour $x$ appartenant à l'intervalle $\left]0~;~\dfrac{1}{\alpha}\right[$, on a $f\left(\dfrac{1}{x}\right) > 0$.
- On admet le tableau de signes suivant :
En déduire le tableau de variations de $g$ sur l'intervalle $]0~;~1]$. Les images et les limites ne sont pas demandées.

Partie C : un calcul d'aire
On a représenté sur le graphique ci-dessous :
- La courbe $\mathcal{C}_{g}$ de la fonction $g$ ;
- La parabole $\mathcal{P}$ d'équation $y = -\dfrac{7}{8}x^{2} + x$ sur l'intervalle $]0~;~1]$.
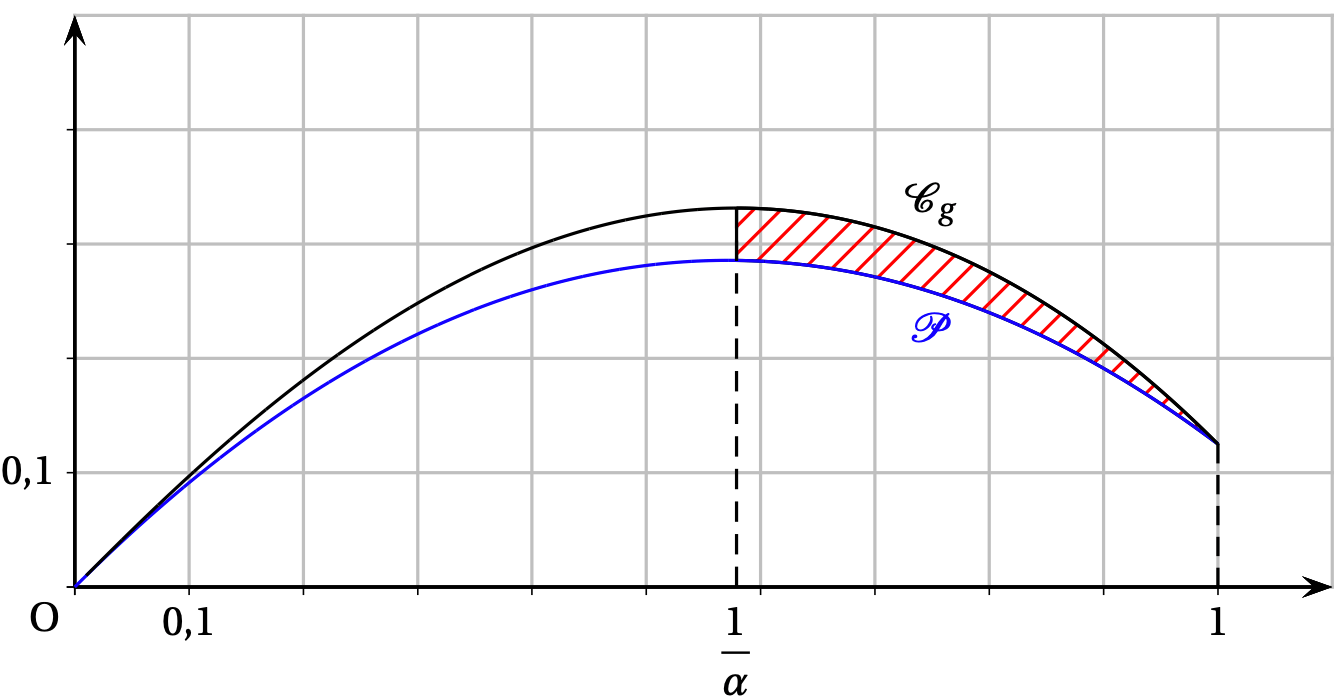
On souhaite calculer l'aire $\mathcal{A}$ du domaine hachuré compris entre les courbes $\mathcal{C}_{g}$ et $\mathcal{P}$, et les droites d'équations $x = \dfrac{1}{\alpha}$ et $x = 1$.
On rappelle que $\ln(\alpha) = 2(2-\alpha)$.
-
- Justifier la position relative des courbes $\mathcal{C}_{g}$ et $\mathcal{P}$ sur l'intervalle $\left]0~;~1\right]$.
- Démontrer l'égalité :
$$ \int_{\frac{1}{\alpha}}^{1} x^{2} \ln x \,\mathrm{d}x = \dfrac{-\alpha^{3} - 6\alpha + 13}{9\alpha^{3}}. $$
- En déduire l'expression en fonction de $\alpha$ de l'aire $\mathcal{A}$.
Polynesie 19 Juin 2024 Jour 1
1 exercice
Une entreprise fabrique des objets en plastique en injectant dans un moule de la matière fondue à $210$~°C. On cherche à modéliser le refroidissement du matériau à l'aide d'une fonction $f$ donnant la température du matériau injecté en fonction du temps $t$.
Le temps est exprimé en secondes et la température est exprimée en degré Celsius.
On admet que la fonction $f$ cherchée est solution d'une équation différentielle de la forme suivante où $m$ est une constante réelle que l'on cherche à déterminer :
$$ (E) : ~ y' +0,02y = m. $$
Partie A
- Justifier l'affichage suivant d'un logiciel de calcul formel :
Entrée : RésoudreEquationDifférentielle $(y' + 0,02y = m)$ Sortie : $\to y = k \cdot \exp(-0.02 \cdot t) + 50 \cdot m$ - La température de l'atelier est de $30$°C. On admet que la température $f(t)$ tend vers $30$°C lorsque $t$ tend vers l'infini.
Démontrer que $m = 0,6$. - Déterminer l'expression de la fonction $f$ cherchée en tenant compte de la condition initiale $f(0) = 210$.
Partie B
On admet ici que la température (exprimée en degré Celsius) du matériau injecté en fonction du temps (exprimé en seconde) est donnée par la fonction dont l'expression et une représentation graphique sont données ci-dessous :
$$ f(t) =180 e^{-0,02t} + 30. $$
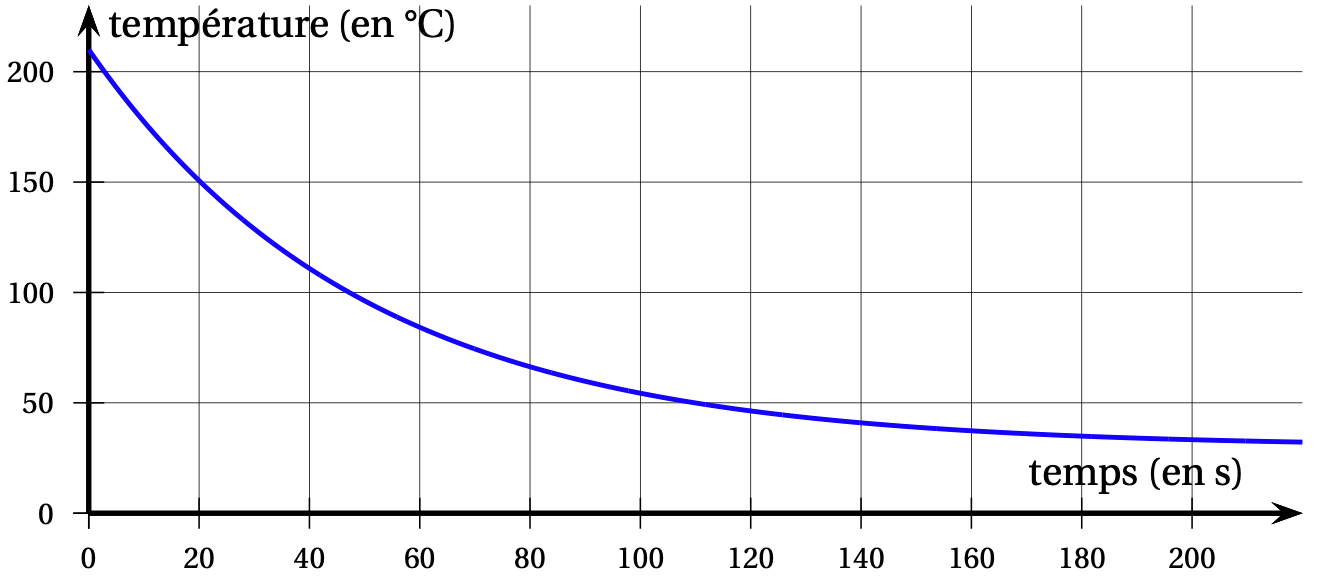
- L'objet peut être démoulé lorsque sa température devient inférieure à $50$°C.
- Par lecture graphique, donner une valeur approchée du nombre $T$ de secondes à attendre avant de démouler l'objet.
- Déterminer par le calcul la valeur exacte de ce temps $T$.
- À l'aide d'une intégrale, calculer la valeur moyenne de la température sur les $100$ premières secondes.
Polynesie 20 Juin 2024 Jour 2
1 exercice
Cet exercice est un questionnaire à choix multiples (QCM) qui comprend cinq questions. Les cinq questions sont indépendantes.
Pour chacune des questions, une seule des quatre réponses est exacte. Le candidat indiquera sur sa copie le numéro de la question suivi de la lettre correspondant à la réponse exacte.
Aucune justification n'est demandée.
Une réponse fausse, une réponse multiple ou une absence de réponse ne rapporte, ni n'enlève aucun point.
- La solution $ f $ de l'équation différentielle $ y'=-3y+7 $ telle que $ f(0)=1 $ est la fonction définie sur $ \mathbb{R} $ par :
- $ f(x) = e^{-3x} $
- $ f(x) = - \dfrac{4}{3} e^{-3x} + \dfrac{7}{3} $
- $ f(x) = e^{-3x} + \dfrac{7}{3} $
- $ f(x) = - \dfrac{10}{3} e^{-3x} - \dfrac{7}{3} $
-
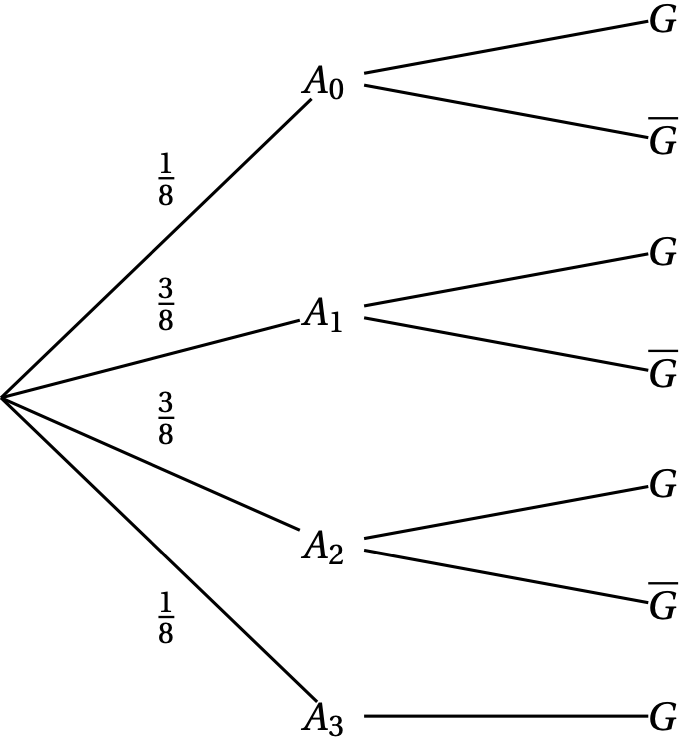
- On considère la fonction $ g $ définie sur $ \mathbb{R} $ par $ g(x) = x^2 \ln \left(x^2 + 4\right) $.
Alors $ \displaystyle\int_0^2 g'(x)\:\text{d}x $ vaut, à $ 10^{-1} $ près :- 4,9
- 8,3
- 1,7
- 7,5
- Une professeure enseigne la spécialité mathématiques dans une classe de 31 élèves de terminale.
Elle veut former un groupe de 5 élèves. De combien de façons différentes peut-elle former un tel groupe de 5 élèves ?- $ 31^5 $
- $ 31\times30\times29\times28\times27 $
- $ 31+30+29+28+27 $
- $ \dbinom{31}{5} $
- La professeure s'intéresse maintenant à l'autre spécialité des 31 élèves de son groupe :
- 10 élèves ont choisi la spécialité physique-chimie ;
- 20 élèves ont choisi la spécialité SES ;
- 1 élève a choisi la spécialité LLCE espagnol.
Elle veut former un groupe de 5 élèves comportant exactement 3 élèves ayant choisi la spécialité SES. De combien de façons différentes peut-elle former un tel groupe ?
- $ \displaystyle\binom{20}{3} \times \binom{11}{2} $
- $ \displaystyle\binom{20}{3} + \binom{11}{2} $
- $ \displaystyle\binom{20}{3} $
- $ 20^3 \times 11^2 $
Contenu Premium
Cette vidéo explicative fait partie de notre contenu premium. Abonnez-vous pour accéder à toutes les méthodes détaillées.
Avec l'abonnement premium :
- Vidéos explicatives détaillées
- Accès à toutes les méthodes
- Exercices corrigés inclus
- Support prioritaire