Contrôles d'entraînement
sur 1 exercice complété
Lorsque la queue d’un lézard des murailles casse elle repousse toute seule en une soixantaine de jours. Lors de la repousse on modélise la longueur en centimètre de la queue du lézard en fonction du nombre de jours.
Cette longueur est définie par la fonction $f$ définie sur $[0;+\infin[$ par,
$$f(x)=10e^u(x)$$où $u$ est la fonction définie sur $[0;+\infin[$ par,
$$u(x)=-e^{2-\frac{x}{10}}$$On admet que la fonction $f$ est dérivable sur $[0;+\infin[$
- Vérifier que pour tout $x$ positif on a $f'(x)=-u(x)e^{u(x)}$. En déduire le sens de variations de la fonction f sur $[0;+\infin[$.
- Calculer $f(20)$. En déduire une estimation, arrondie au millimètre, de la queue du lézard après vingt jours de repousse.
- Selon cette modélisation, la queue du lézard peut-elle mesurer 11 cm ?
- On souhaite déterminer au bout de combien de jours la vitesse de croissance est maximale. On admet que la vitesse de croissance au bout de $x$ jours est donnée par $f'(x)$. On admet que la fonction dérivée $f'$ est dérivable sur $[0;+\infin[$, on note $f''$ la fonction dérivée de $f'$ et on admet que:$$f''(x)=\frac{1}{10}u(x)e^{u(x)}(1+u(x))$$
- Déterminer les variations de $f'$ sur $[0;+\infin[$.
- En déduire la convexité de $f$ sur $[0;+\infin[$ et les potentiels point d'inflexion.
- Au bout de combien de jours la vitesse de croissance de la longueur de la queue du lézard est maximale?
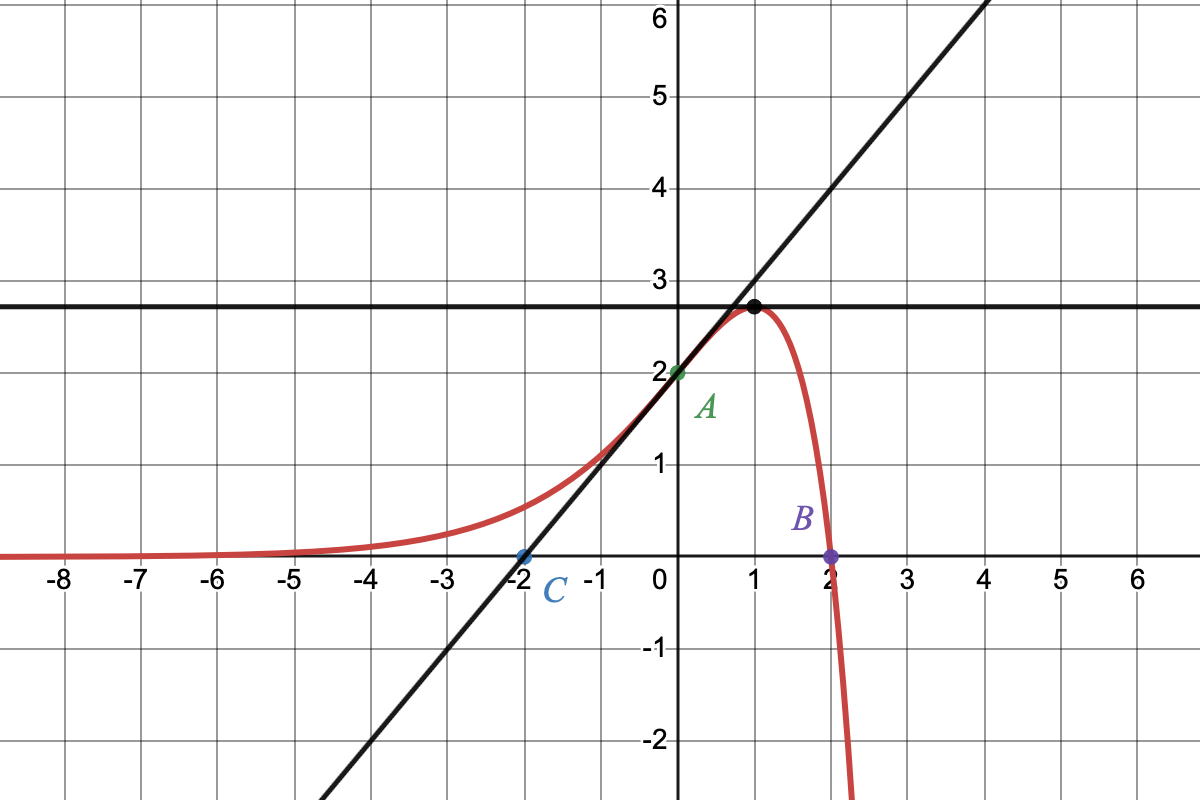
- Indiquer les valeurs de $f(0)$ et de $f(2)$.
- Indiquer la valeur de $f'(1)$.
- Donner une équation de la tangente à la courbe $C_f$ au point $A$.
- Indiquer le nombre de solutions de l'équation $f(x)=1$ dans l'intervalle $[-10 ; 2]$.
- Indiquer les variations de la fonction $f$ sur l'intervalle $[-10 ; 2]$.
- Déterminer l'intervalle sur lequel la fonction $f$ est convexe, et celui sur lequel elle est concave, ainsi que les éventuels points d'inflexion.
Dans le repère ci-dessous, on note $C_f$ la courbe représentative d'une fonction $f$ définie sur l'intervalle $[-10 ; 2]$. On a placé les points $A(0; 2)$, $B(2; 0)$ et $C(-2; 0)$. On dispose des renseignements suivants: Le point $B$ appartient à la courbe $C_f$ . La droite $(AC)$ est tangente en $A$ à la courbe $C_f$. La tangente à la courbe $C_f$ au point d'abscisse $1$ est une droite horizontale.
PARTIE A
Répondre aux questions suivantes par lecture graphique.
PARTIE B
Reprendre les questions de la partie A par le calcul, sachant que $f(x)=(2-x)e^x$.
Contenu Premium
Cette vidéo explicative fait partie de notre contenu premium. Abonnez-vous pour accéder à toutes les méthodes détaillées.
Avec l'abonnement premium :
- Vidéos explicatives détaillées
- Accès à toutes les méthodes
- Exercices corrigés inclus
- Support prioritaire
Dérivation et convexité
Fiche de synthèse
Compléments sur la dérivation
| Condition | Formule |
| $u$ est dérivable sur $I$, $n \in \Z$ n si $n<0$, $u$ ne doit pas s'annuler |
$(u^n)'=n\times u^{n-1}\times u'$ |
| $u$ est dérivable et ne s'annule pas sur $I$ | $(\dfrac{1}{u})'=\dfrac{-1}{u^2}$ |
| $u$ est strictement positive et dérivable sur un intervalle $I$ | $(\sqrt{u})'=\dfrac{u'}{2\sqrt{u}}$ |
| $u$ est dérivable sur un intervalle $I$ | $(e^{u})'=u'\times e^u$ |
Contenu Complet Premium
Pour accéder au contenu complet de cette fiche de cours, vous devez vous abonner à notre offre premium.
Avec l'abonnement premium :
- Fiches de cours complètes
- Accès à toutes les méthodes
- Exercices corrigés inclus
- Vidéos explicatives détaillées


